题目内容
 如图,DG∥AB,DG=AG,∠1=∠2;
如图,DG∥AB,DG=AG,∠1=∠2;(1)判断EF与AD是否平行?说明你的理由.
(2)若∠BAC=70°,求∠FEA的度数.
分析:(1)由DG∥AB,可得∠1=∠3,则∠2=∠3,所以EF∥AD;
(2)由已知易得AD平分∠BAC,则∠3=35°,再利用两直线平行,同旁内角互补求解即可.
(2)由已知易得AD平分∠BAC,则∠3=35°,再利用两直线平行,同旁内角互补求解即可.
解答:解:(1)判断:EF∥AD(1分)
理由:∵DG∥AB,
∴∠1=∠3,(1分)
又∵∠1=∠2,
∴∠2=∠3,
∴EF∥AD;(1分)
(2)∵DG=AG,
∴∠1=∠GAD,(1分)
又∵∠1=∠3,
∴∠3=
∠BAC=
×70°=35°,(1分)
∵EF∥AD,
∴∠FEA=180°-∠3=145°.(1分)
理由:∵DG∥AB,
∴∠1=∠3,(1分)
又∵∠1=∠2,
∴∠2=∠3,
∴EF∥AD;(1分)
(2)∵DG=AG,
∴∠1=∠GAD,(1分)
又∵∠1=∠3,
∴∠3=
| 1 |
| 2 |
| 1 |
| 2 |
∵EF∥AD,
∴∠FEA=180°-∠3=145°.(1分)
点评:此题考查平行线的判定和性质:同位角相等,两直线平行;两直线平行,同旁内角互补,要灵活应用.

练习册系列答案
相关题目
 15、已知:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.
15、已知:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB. 23、已知:如图,CD⊥AB于D,点E为BC边上的任意一点,EF⊥AB于F,且∠1=∠2,那么BC与DG平行吗?请说明理由.
23、已知:如图,CD⊥AB于D,点E为BC边上的任意一点,EF⊥AB于F,且∠1=∠2,那么BC与DG平行吗?请说明理由.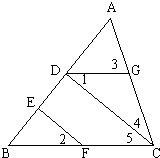 20、已知:如图,CD⊥AB,垂足为D,点F是BC上任意一点,FE⊥AB,垂足为E,且∠1=∠2=30°,∠3=84°,求∠4的度数.
20、已知:如图,CD⊥AB,垂足为D,点F是BC上任意一点,FE⊥AB,垂足为E,且∠1=∠2=30°,∠3=84°,求∠4的度数. 如图,DG∥AB,DG=AG,∠1=∠2;
如图,DG∥AB,DG=AG,∠1=∠2;