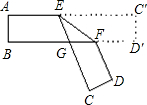
题目内容
如图，将矩形纸片ABCD（AD＞DC）的一角沿着过点D的直线折叠，使点A落在BC边上，落点为E，折痕交AB边交于点F；若BE：EC=m：n，则AF：FB=______（用含有m、n的代数式表示）
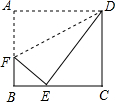
∵∠DEF=90°，∴∠BEF+∠CED=90°．
又∠BEF+∠BFE=90°，
∴∠BFE=∠CED．又∠B=∠C，
△BEF∽△CDE．
∴EF：FB=DE：EC．
∵BE：EC=m：n，
∴可设BE=mk，EC=nk，则DE=（m+n）k．
∴
=
=
=
．
∵AF=EF，
∴AF：FB=
．
故答案为：
．
又∠BEF+∠BFE=90°，
∴∠BFE=∠CED．又∠B=∠C，
△BEF∽△CDE．
∴EF：FB=DE：EC．
∵BE：EC=m：n，
∴可设BE=mk，EC=nk，则DE=（m+n）k．
∴
| EF |
| FB |
| DE |
| EC |
| (m+n)k |
| nk |
| m+n |
| n |
∵AF=EF，
∴AF：FB=
| m+n |
| n |
故答案为：
| m+n |
| n |
练习册系列答案
相关题目
，则该车的牌照号码是______．
