题目内容
已知:如图,在∠POQ内部有两点M、N,∠MOP=∠NOQ.
(1)画图并简要说明画法:在射线OP上取一点A,使点A到点M和点N的距离和最小;在射线OQ上取一点 B,使点B到点M和点N的距离和最小;
B,使点B到点M和点N的距离和最小;
(2)直接写出AM+AN与BM+BN的大小关系.
解:(1)画法:
(2)答:AM+AN
(1)画图并简要说明画法:在射线OP上取一点A,使点A到点M和点N的距离和最小;在射线OQ上取一点
 B,使点B到点M和点N的距离和最小;
B,使点B到点M和点N的距离和最小;(2)直接写出AM+AN与BM+BN的大小关系.
解:(1)画法:
(2)答:AM+AN
=
=
BM+BN.(填“>”、“=”或“<”)分析:(1)分别作出点M关于射线OP的对称点M',点N关于射线OQ的对称点N',连接M′N、N′M即可;
(2)利用轴对称性质即可求得两线段和相等.
(2)利用轴对称性质即可求得两线段和相等.
解答:解:(1)答案图如图:
 .
.
画法:1.作点M关于射线OP的对称点M′,
连接M′N交OP于点A.
2作点N关于射线OQ的对称点N′,
④连接N′M交OQ于点B.
(2)
由做法知AM+AN=NM′,BM+BN=N′M.
作射线OM′、ON′.
∵M、M'关于OP对称
∴OM=OM′,∠MOP=∠M′OP
同理,ON=ON′,∠NOQ=∠QON′.
又∵∠MOP=∠NOQ
∴∠MOM′=∠NON′
∴∠NOM′=∠MON′.
∴△N′OM≌△NOM′
∴N′M=NM′,即AM+AN=BM+BN.
故答案为:=.
 .
.画法:1.作点M关于射线OP的对称点M′,
连接M′N交OP于点A.
2作点N关于射线OQ的对称点N′,
④连接N′M交OQ于点B.
(2)

由做法知AM+AN=NM′,BM+BN=N′M.
作射线OM′、ON′.
∵M、M'关于OP对称
∴OM=OM′,∠MOP=∠M′OP
同理,ON=ON′,∠NOQ=∠QON′.
又∵∠MOP=∠NOQ
∴∠MOM′=∠NON′
∴∠NOM′=∠MON′.
∴△N′OM≌△NOM′
∴N′M=NM′,即AM+AN=BM+BN.
故答案为:=.
点评:考查最短路线问题;得到两条线段相等的理由是解决本题的难点.

练习册系列答案
相关题目
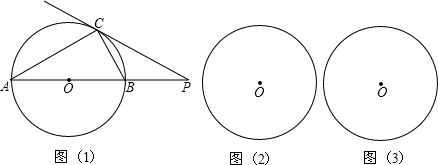
 已知:如图AB是半圆0的直径,点C在半圆上,CD⊥AB,垂足为D,切线PC交BA的延长线于点P,AD,DB的长是关于x的方程x2-(4m+2)+4m2=0(m>0)的两根,且AD:DB=1:4,求:PO、PC的长.
已知:如图AB是半圆0的直径,点C在半圆上,CD⊥AB,垂足为D,切线PC交BA的延长线于点P,AD,DB的长是关于x的方程x2-(4m+2)+4m2=0(m>0)的两根,且AD:DB=1:4,求:PO、PC的长. (2004•西藏)已知,如图,P是⊙O外一点,PC切⊙O于点C,割线PO交⊙O于点B、A,且AC=PC.
(2004•西藏)已知,如图,P是⊙O外一点,PC切⊙O于点C,割线PO交⊙O于点B、A,且AC=PC. ,且PB=2
,且PB=2

