Question

如图，在平面直角坐标系中，点O是坐标原点，四边形AOCB是梯形，AB∥OC，点A的坐标为（0，8），点C的坐标为（10，0），OB=OC．
（1）求点B的坐标；
（2）点P从C点出发，沿线段CO以5个单位/秒的速度向终点O匀速运动，过点P作PH⊥OB，垂足为H，设△HBP的面积为S（S≠0），点P的运动时间为t秒，求S与t之间的函数关系式（直接写出自变量t的取值范围）；
（3）在（2）的条件下，过点P作PM∥CB交线段AB于点M，过点M作MR⊥OC，垂足为R，线段MR分别交直线PH、OB于点E、G，点F为线段PM的中点，连接EF，当t为何值时，？

Answer 1

解：（1）如图1，过点B作BN⊥OC，垂足为N
由题意知OB=OC=10，BN=OA=8
∴ON=，
∴B（6，8）

（2）如图1，∵∠BON=∠POH，∠ONB=∠OHP=90°
∴△BON∽△POH，
∴
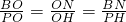
∵PC=5t，
∴OP=10-5t
∴OH=6-3t，PH=8-4t
∴BH=OB-OH=10-（6-3t）=3t+4，
∴S=（3t+4）（8-4t）=-6t²+4t+16（0≤t＜2）

（3）①当点G在点E上方时，
如图2过点B作BN′⊥OC，垂足为N′
BN′=8，CN′=4
∴CB=
∵BM∥PC，BC∥PM
∴四边形BMPC是平行四边形
∴PM=BC=4，BM=PC=5t
∵OC=OB，
∴∠OCB=∠OBC
∵PM∥CB，
∴∠OPD=∠OCB，∠ODP=∠OBC
∴∠OPD=∠ODP
∵∠OPD+∠RMP=90°，∠ODP+∠DPH=90°
∴∠RMP=∠DPH
∴EM=EP
∵点F为PM的中点，
∴EF⊥PM
∵∠EFM=∠PRM=∠EMF+∠PMR=90°
∴△MEF∽△MPR
∴，其中MF=
MR=8，PR=
∴ME=5，EF=
∵，
∴EG=2
∴MG=EM-EG=5-2=3
∵AB∥OC
∴∠MBG=∠BON′
又∵∠GMB=∠ON′B=90°
∴△MGB∽△N′BO
∴，
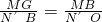∴BM=
∴5t=
∴t=

②当点G在点E下方时，如图3，同理可得MG=ME+EG=5+2=7
∴BM=5t=，
∴t=
∴当t=或t=时，
．
分析：（1）过点B作BN⊥OC，则四边形ABNO是矩形，BN=AO=8，AB=ON，由勾股定理可求得NB的长；
（2）可证△BON∽△POH，有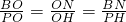，由题意知OP=10-5t，OH=6-3tPH=8-4t，BH=OB-OH=10-（6-3t）=3t+4，从而求得S的表达式，由于OC=10，故0≤t＜2；
（3）分两种情况分析：①当点G在点E上方时，如图2过点B作BN′⊥OC，垂足为N′，先得到四边形BMPC是平行四边形，有PM=BC=4，BM=PC=5t，证得∠OPD=∠ODP，由同角的余角相等得到∠RMP=∠DPH，有EM=EP，由于点F为PM的中点，则EF⊥PM，得到∠EMF=∠PMR，∠EFM=∠PRM=90°，有△MEF∽△MPR，有，由条件可得ME=5，EF=，根据题意知，有EG=2，MG=EM-EG=5-2=3，又可证得△MGB∽△N′BO，有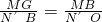，得BM=，从而求得t的值；②当点G在点E下方时，如图3，同理可得MG=ME+EG=5+2=7，有BM=5t=，可得t的值．
点评：本题主要考查了相似三角形的判定和性质，勾股定理以及平行四边形的性质，平面直角坐标每等知识点，要注意（3）中，要分类讨论，从而得出运动时间t的值．不要忽略掉任何一种情况．