题目内容
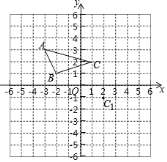
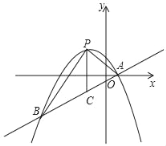
【题目】如图,抛物线![]() 与坐标轴分别交于点
与坐标轴分别交于点![]()
![]() ,点P是线段AB上方抛物线上的一个动点。
,点P是线段AB上方抛物线上的一个动点。
(1)当点P运动到什么位置时,![]() 的面积有最大值?
的面积有最大值?
(2)过点P作![]() 轴的垂线,交线段AB于点D,再过点P作
轴的垂线,交线段AB于点D,再过点P作![]() 交抛物线于点E,连接DE,请问是否存在点P使
交抛物线于点E,连接DE,请问是否存在点P使![]() 为等腰直角三角形?若存在,直接写出点P的坐标;若不存在,说明理由。
为等腰直角三角形?若存在,直接写出点P的坐标;若不存在,说明理由。
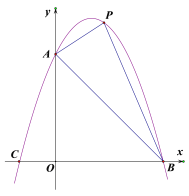

【答案】(1)点P运动到P![]() 时,时,ΔPAB的面积有最大值;(2)
时,时,ΔPAB的面积有最大值;(2)![]() 或
或![]() .
.
【解析】
(1)先用待定系数法求解可得抛物线函数解析式;然后作PM⊥OB与点M,交AB于点N,作AG⊥PM,先求出直线AB解析式为y=-x+6,设P(t,-![]() t2+2t+6),则N(t,-t+6),由S△PAB=S△PAN+S△PBN=
t2+2t+6),则N(t,-t+6),由S△PAB=S△PAN+S△PBN=![]() PNAG+
PNAG+![]() PNBM=
PNBM=![]() PNOB列出关于t的函数表达式,利用二次函数的性质求解可得;
PNOB列出关于t的函数表达式,利用二次函数的性质求解可得;
(2)若△PDE为等腰直角三角形,则PD=PE,设点P的横坐标为a,表示出PD、PE的长,列出关于a的方程,解之可得答案.
解:(1)∵抛物线过点B(6,0)、C(-2,0),
∴设抛物线解析式为y=a(x-6)(x+2),
将点A(0,6)代入,得:-12a=6,
解得:a=-![]() ,
,
所以抛物线解析式为y=-![]() (x-6)(x+2)=-
(x-6)(x+2)=-![]() x2+2x+6;
x2+2x+6;
如图1,过点P作PM⊥OB与点M,交AB于点N,作AG⊥PM于点G,
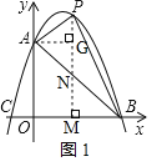
设直线AB解析式为y=kx+b,
将点A(0,6)、B(6,0)代入,得:
![]() ,
,
解得:![]() ,
,
则直线AB解析式为y=-x+6,
设P(t,-![]() t2+2t+6)其中0<t<6,
t2+2t+6)其中0<t<6,
则N(t,-t+6),
∴PN=PM-MN=-![]() t2+2t+6-(-t+6)=-
t2+2t+6-(-t+6)=-![]() t2+2t+6+t-6=-
t2+2t+6+t-6=-![]() t2+3t,
t2+3t,
∴S△PAB=S△PAN+S△PBN
=![]() PNAG+
PNAG+![]() PNBM
PNBM
=![]() PN(AG+BM)
PN(AG+BM)
=![]() PNOB
PNOB
=![]() ×(-
×(-![]() t2+3t)×6
t2+3t)×6
=-![]() t2+9t
t2+9t
=-![]() (t-3)2+
(t-3)2+![]() ,
,
∴当t=3时,P位于(3,![]() )时,△PAB的面积有最大值;
)时,△PAB的面积有最大值;
(3)如图,
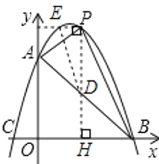
若△PDE为等腰直角三角形,
则PD=PE,
设点P的横坐标为a,点E的横坐标为b,
∵![]() ,
,
∴b=4-a,
∴PE=|a-(4-a)|=|2a-4|=2|2-a|,
又∵PD=-![]() a2+2a+6-(-a+6)=-
a2+2a+6-(-a+6)=-![]() a2+3a,
a2+3a,
∴-![]() a2+3a=2|2-a|,
a2+3a=2|2-a|,
解得:a=4或a=5-![]() ,
,
所以P(4,6)或P(5-![]() ,3
,3![]() -5).
-5).

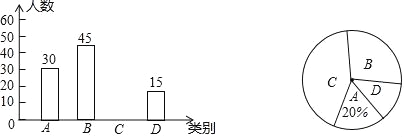
【题目】“学而时习之,不亦乐乎!”,古人把经常复习当作是一种乐趣,能达到这种境界是非常不容易的。复习可以让遗忘的知识得到补拾,零散的知识变得系统,薄弱的知识有所强化,掌握的知识更加巩固,生疏的技能得到训练。为了了解初一学生每周的复习情况,教务处对初一(1)班学生一周复习的时间进行了调查,复习时间四舍五入后只有4种:1小时,2小时,3小时,4小时,一周复习2小时的女生人数占全班人数的16%,一周复习4小时的男女生人数相等。根据调查结果,制作了两幅不完整的统计图(表):
初一(1)班女生复习时间数据(单位:小时) | |||||||||
0.9 | 1.3 | 1.7 | 1.8 | 1.9 | 2.2 | 2.2 | 2.2 | 2.3 | 2.4 |
3.2 | 3.2 | 3.2 | 3.3 | 3.8 | 3.9 | 3.9 | 4.1 | 4.2 | 4.3 |
女生一周复习时间频数分布表 |
| |
分组(四舍五入)后) | 频数(学生人数) | |
1小时 | 2 | |
2小时 | a | |
3小时 | 4 | |
4小时 | b | |
(1)四舍五入前,女生一周复习时间的众数为 小时,中位数为 小时;
(2)统计图中a = ,c = ,初一(1)班男生人数为 人,根据扇形统计图估算初一(1)班男生的平均复习时间为 小时;
(3)为了激励学生养成良好的复习习惯,教务处决定对一周复习时间四舍五入后达到3小时及以上的全年级学生进行表扬,每人奖励1个笔记本,初一年级共有1000名学生,请问教务处应该准备大约多少个笔记本?
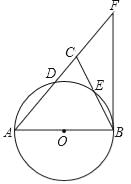
【题目】电影公司随机收集了电影的有关数据,经分类整理得到下表:
电影类型 | 第一类 | 第二类 | 第三类 | 第四类 | 第五类 | 第六类 |
电影部数 | 140 | 50 | 300 | 200 | 800 | 510 |
获得好评的电影部数 | 56 | 10 | 45 | 50 | 160 | 51 |
(1)从电影公司收集的电影中随机选取1部,求这部电影是获得好评的第四类电影的概率:
(2)电影公司为增加投资回报,需在调查前根据经验预估每类电影的好评率(好评率是指:一类电影中获得好评的部数与该类电影的部数的比值),如表所示:
电影类型 | 第一类 | 第二类 | 第三类 | 第四类 | 第五类 | 第六类 |
预估好评率 | 0.5 | 0.2 | 0.15 | 0.15 | 0.4 | 0.3 |
定义统计最![]() 其中
其中![]() 为第i类电影的实际好评率,
为第i类电影的实际好评率,![]() 为第i类电影的预估好评率(i=1,2,...,n).规定:若S<0.05,则称该次电影的好评率预估合理,否则为不合理,判断本次电影的好评率预估是否合理。
为第i类电影的预估好评率(i=1,2,...,n).规定:若S<0.05,则称该次电影的好评率预估合理,否则为不合理,判断本次电影的好评率预估是否合理。