题目内容
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2﹣![]() x+
x+![]() 与直线y=
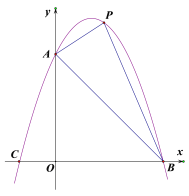
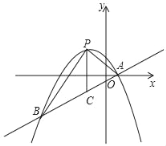
与直线y=![]() x+b交于A、B两点,其中点A在x轴上,点P是直线AB上方的抛物线上一动点(不与点A、B重合)过P作y轴的平行线交直线于点C,连接PA、PB.
x+b交于A、B两点,其中点A在x轴上,点P是直线AB上方的抛物线上一动点(不与点A、B重合)过P作y轴的平行线交直线于点C,连接PA、PB.
(1)求直线的解析式及A、B点的坐标;
(2)当△APB面积最大时,求点P的坐标以及最大面积.
【答案】(1)y=![]() x﹣
x﹣![]() ,A点的坐标为(1,0),B点的坐标为(﹣5,﹣3);(2)当x=﹣2时,△APB面积最大,最大值为27,此时点P的坐标为(﹣2,
,A点的坐标为(1,0),B点的坐标为(﹣5,﹣3);(2)当x=﹣2时,△APB面积最大,最大值为27,此时点P的坐标为(﹣2,![]() ).
).
【解析】
(1)令![]() =0求出A点的坐标,将A点坐标代入y=
=0求出A点的坐标,将A点坐标代入y=![]() x+b可求出直线解析式,联立抛物线和直线解析式可求出B点的坐标;
x+b可求出直线解析式,联立抛物线和直线解析式可求出B点的坐标;
(2)设P(x,![]() ),则C(x,
),则C(x,![]() x﹣
x﹣![]() ),由此表示出PC的长,根据三角形面积公式得到S△APB=
),由此表示出PC的长,根据三角形面积公式得到S△APB=![]() (﹣x2﹣4x+5)×(1+5),整理成顶点式,即可求出面积最大值和P的坐标.
(﹣x2﹣4x+5)×(1+5),整理成顶点式,即可求出面积最大值和P的坐标.
(1)∵y=![]() ,
,
∴当y=0时,![]() =0,
=0,
解得x1=﹣![]() ,x2=1,
,x2=1,
∴A点的坐标为(1,0).
将A(1,0)代入y=![]() x+b,
x+b,
得0=![]() ×1+b,
×1+b,
解得b=﹣![]() ,
,
∴直线的解析式为y=![]() x﹣
x﹣![]() .
.
由 ,解得
,解得![]() ,
,![]() ,
,
∴B点的坐标为(﹣5,﹣3);
(2)设P(x,![]() ),则C(x,
),则C(x,![]() x﹣
x﹣![]() ),
),
∴PC=(![]() )﹣(
)﹣(![]() x﹣
x﹣![]() )=﹣x2﹣4x+5,
)=﹣x2﹣4x+5,
∴S△APB=![]() PC|xA﹣xB|
PC|xA﹣xB|
=![]() (﹣x2﹣4x+5)×(1+5)
(﹣x2﹣4x+5)×(1+5)
=﹣3x2﹣12x+15
=﹣3(x+2)2+27,
当x=﹣2时,△APB面积最大,最大值为27,此时点P的坐标为(﹣2,![]() ).
).

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目