题目内容
一船在灯塔C的正东方向8海里的A处,以20海里/小时的速度沿北偏西30°方向行驶.
(1)经过多长时间,船距灯塔最近?
(2)经过多长时间,船到灯塔的正北方向?此时船距灯塔有多远?
(1)经过多长时间,船距灯塔最近?
(2)经过多长时间,船到灯塔的正北方向?此时船距灯塔有多远?
分析:(1)根据方向角可知∠CAD=60°,由三角函数可求AD的长,根据时间=路程÷速度,列式计算即可求解;
(2)根据三角函数可求AE,CE的长,根据时间=路程÷速度,列式计算即可求解.
(2)根据三角函数可求AE,CE的长,根据时间=路程÷速度,列式计算即可求解.
解答: 解:(1)∠CAD=90°-30°=60°,
解:(1)∠CAD=90°-30°=60°,
∴AD=AC•cos∠CAD=4海里,
4÷20=
(小时).
答:经过
小时,船距灯塔最近.
(2)AE=AC÷cos∠CAD=16海里,
16÷20=0.8(小时),
CE=AC•tan∠CAD=8
海里.
答:经过
小时,船到灯塔的正北方向,此时船距灯塔8
海里.
 解:(1)∠CAD=90°-30°=60°,
解:(1)∠CAD=90°-30°=60°,∴AD=AC•cos∠CAD=4海里,
4÷20=
| 1 |
| 5 |
答:经过
| 1 |
| 5 |
(2)AE=AC÷cos∠CAD=16海里,
16÷20=0.8(小时),
CE=AC•tan∠CAD=8
| 3 |
答:经过
| 4 |
| 5 |
| 3 |
点评:考查了方向角和三角函数的应用,本题的关键是画出图形,求得相应的线段的长度.

练习册系列答案
相关题目
 一艘船向正东方先航行,上午10点在灯塔P的西南方向a海里处,到下午2点时航行到灯塔的东偏南60°的方向,求出船的航行速度.
一艘船向正东方先航行,上午10点在灯塔P的西南方向a海里处,到下午2点时航行到灯塔的东偏南60°的方向,求出船的航行速度. 一船在A处测得北偏东45°方向有一灯塔B,船向正东方向以每小时20海里的速度航行1.5小时到达C处时,又观测到灯塔B在北偏东15°方向上,求此时航船与灯塔相距多少海里?
一船在A处测得北偏东45°方向有一灯塔B,船向正东方向以每小时20海里的速度航行1.5小时到达C处时,又观测到灯塔B在北偏东15°方向上,求此时航船与灯塔相距多少海里?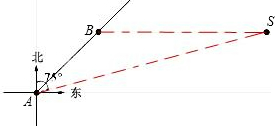 船可以继续沿东北方向航行吗?为什么?(参考数据:
船可以继续沿东北方向航行吗?为什么?(参考数据:
