题目内容
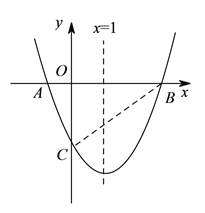
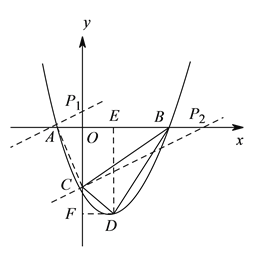
【题目】如图，已知抛物线
的对称轴为直线
，（ 
），且经过
、
两点，与
轴交于另一点
，设
是抛物线的对称轴
上的一动点，且
．
（
）求这条抛物线所对应的函数关系式．
（
）求点
的坐标．
（
）探究坐标轴上是否存在点
，使得
、
、
为顶点的三角形与
相似？若存在，请指出符合条件的点
的位置，并直接写出点
的坐标；若不存在，请说明理由．
【答案】（1）
；（2）
；（3）
， 
， 
【解析】解：（
）设该抛物线的解析式为
，
由抛物线与
轴交于点
，可知
，
即抛物线的解析式为
，
把
、
代入，
得
解得
， 
．
∴抛物线的解析式为
；
（
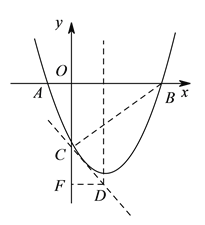
）设经过
点且与直线
垂直的直线为直线
，作
轴，垂足为
；
∵
，
∴
， 
，
∴
．
（
）连接
，则容易得出
，又
，可知
，得符合条件的点为
．
过
作
交
轴正半轴于
，可知
，
求得符合条件的点为
．
过
作
交
轴正半轴于
，可知
，
求得符合条件的点为
．
∴符合条件的点有三个： 
， 
， 
．
练习册系列答案
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
相关题目
