题目内容
若记y=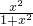
=f（x），如f（1）表示x=1时y的值，即f（1）=
=
，则f（2010）+f（2009）+…+f（2）+f（1）+f（）+…+f（
）+f（
）=______．
解：∵y=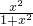=f（x），
∴f（2010）+f（2009）+…+f（2）+f（1）+f（）+…+f（）+f（）
=f（2010）+f（）+f（2009）+f（+…+f（2）+f（）+f（1）
=2009．
故答案为：2009．
分析：根据互为倒数的两个数的函数值的和等于1，依此可得f（2010）+f（2009）+…+f（2）+f（1）+f（）+…+f（）+f（）=1×2009+=2009．
点评：本题考查了规律型：数字的变化和函数值，得出互为倒数的两个数的函数值的和等于1是解题的关键．
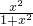=f（x），∴f（2010）+f（2009）+…+f（2）+f（1）+f（
）+…+f（）+f（）=f（2010）+f（
）+f（2009）+f（+…+f（2）+f（）+f（1）=2009
．故答案为：2009
．分析：根据互为倒数的两个数的函数值的和等于1，依此可得f（2010）+f（2009）+…+f（2）+f（1）+f（
）+…+f（）+f（）=1×2009+=2009．点评：本题考查了规律型：数字的变化和函数值，得出互为倒数的两个数的函数值的和等于1是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图，已知A1，A2，A3，…，A2006是x轴上的点，且OA1=A1A2=A2A3=…=A2005A2006=1，分别过点A1，A2，A3，…，A2006作x轴的垂线交二次函数y=x2（x≥0）的图象于点P1，P2，P3，…，P2006点，若记△OA1P1的面积为S1，过点P1作P1B1⊥A2P2于点B1，记△P1B1P2的面积为S2，过点P2作P2B2⊥A3P3于点B2，记△P2B2P3的面积为S3，…，依次进行下去，最后记△P2005B2005P2006的面积为S2006，则S2006-S2005=
某公司出纳员小张在办理业务时，约定收入为正，支出为负，今年10月的某一天，他先后办理了七笔业务：+2000元、-800元、+400元、-800元、+1400元、-1600元、-200元，