题目内容
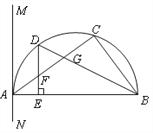
【题目】如图,直线![]() 过点A(0,6),点D(8,0),直线
过点A(0,6),点D(8,0),直线![]() :
:![]() 与
与![]() 轴交于点C,两直线
轴交于点C,两直线![]() ,
,![]() 相交于点B.
相交于点B.
(1)求直线![]() 的解析式和点B的坐标;
的解析式和点B的坐标;
(2)连接AC,求![]() 的面积;
的面积;
(3)若在AD上有一点P,把线段AD分成2:3的两部分时,请直接写出点P的坐标(不必写解答过程).

【答案】(1)直线![]() 的解析式为
的解析式为![]() ,
,![]() ;(2)15;(3)点P的坐标为
;(2)15;(3)点P的坐标为![]() 或
或![]() .
.
【解析】
(1)先利用待定系数法可求出直线![]() 的解析式,再联立直线
的解析式,再联立直线![]() ,
,![]() 的解析式可得点B的坐标;
的解析式可得点B的坐标;
(2)先根据直线![]() 的解析式求出点C的坐标,再根据点
的解析式求出点C的坐标,再根据点![]() 的坐标分别求出
的坐标分别求出![]() 的长以及点B到x轴的距离,然后根据
的长以及点B到x轴的距离,然后根据![]() 的面积等于
的面积等于![]() 的面积减去
的面积减去![]() 的面积即可得;
的面积即可得;
(3)设点P的坐标为![]() ,先利用两点之间的距离公式求出AD的长,再根据题意可得
,先利用两点之间的距离公式求出AD的长,再根据题意可得![]() 或
或![]() ,然后利用两点之间的距离公式分别列出等式,求解即可得.
,然后利用两点之间的距离公式分别列出等式,求解即可得.
(1)设直线![]() 的解析式为
的解析式为![]()
∵直线![]() 经过
经过![]()
∴将点![]() 代入解析式得:
代入解析式得:![]()
解得
则直线![]() 的解析式为
的解析式为![]()
联立![]() ,
,![]() 的解析式得:
的解析式得:
解得![]()
则点B的坐标为![]() ;
;
(2)对于直线![]() :
:![]()
当![]() 时,
时,![]() ,解得
,解得![]()
则点C的坐标为![]()
![]()
![]() ,点B到x轴的距离为3
,点B到x轴的距离为3
则![]()
![]()
![]()
即![]() 的面积为15;
的面积为15;
(3)由题意,设点P的坐标为![]() ,且
,且![]()
![]()
![]()
![]() 点P把线段AD分成
点P把线段AD分成![]() 的两部分
的两部分
![]() 或
或![]()
①当![]() 时
时
由两点之间的距离公式得:![]()
解得![]()
![]()
则此时点P的坐标为![]()
②当![]() 时
时
由两点之间的距离公式得:![]()
解得![]()
![]()
则此时点P的坐标为![]()
综上,点P的坐标为![]() 或
或![]() .
.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目