题目内容
4.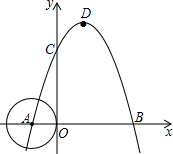 如图,抛物线y=-(x+1)(x-3)交x轴于点A、B,点D为抛物线的顶点,⊙A与y轴相切,现将该圆沿抛物线从点A平移到点D,则圆上的一条直径扫过的最大面积是4$\sqrt{5}$.
如图,抛物线y=-(x+1)(x-3)交x轴于点A、B,点D为抛物线的顶点,⊙A与y轴相切,现将该圆沿抛物线从点A平移到点D,则圆上的一条直径扫过的最大面积是4$\sqrt{5}$.
分析 一条直径扫过的面积是一个曲边平行四边形(一组对边是直径,另一组对过是A到D的那段抛物线),它的面积就等于两条直径为对边的平行四边形的面积,底是确定的直径为2,当高是AD时(即这条直径与线段AD垂直时)面积最大,进而求出即可.
解答 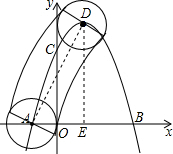 解:如图所示:过点D作DE⊥x轴于点E,
解:如图所示:过点D作DE⊥x轴于点E,
y=-(x+1)(x-3)
=-x2+2x+3
=-(x-1)2+4,
则D(1,4),
y=0时,0=-(x+1)(x-3)
解得:x1=-1,x2=3,
则AO=1,则圆A的直径为2,
则AE=2,DE=4,
故AD=2$\sqrt{5}$,所以最大面积是:2×2$\sqrt{5}$=4$\sqrt{5}$.
故答案为:4$\sqrt{5}$.
点评 此题主要考查了圆的综合以及二次函数综合,根据题意得出这条直径与线段AD垂直时扫过的面积最大是解题关键.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
13.已知三条线段a,b,c,能构成三角形的是( )
| A. | a=3x,b=5x,c=2x(x>0) | B. | a=4,b=1,c=6 | ||
| C. | a=2$\sqrt{3}$,b=3$\sqrt{3}$,c=4$\sqrt{3}$ | D. | a=1.5k,b=2.5k,c=4k(k>0) |
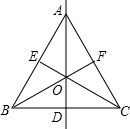 如图是一个轴对称图形,AD所在的直线是对称轴,仔细观察图形,回答下列问题:
如图是一个轴对称图形,AD所在的直线是对称轴,仔细观察图形,回答下列问题: 一次函数y=-$\frac{3}{4}$x+6的图象,交x轴于点A,交y轴于点B.
一次函数y=-$\frac{3}{4}$x+6的图象,交x轴于点A,交y轴于点B.