题目内容
3.已知函数满足下列两个条件:①x>0时,y随x的增大而增大;
②它的图象经过点(1,2).
请写出一个符合上述条件的函数的表达式y=2x(答案不唯一).
分析 根据y随着x的增大而增大推断出k与0的关系,再利用过点(1,2)来确定函数的解析式.
解答 解:∵y随着x的增大而,增大
∴k>0.
又∵直线过点(1,2),
∴解析式为y=2x或y=x+1等.
故答案为:y=2x(答案不唯一).
点评 此题考查了一次函数的性质及正比例函数的性质,在y=kx+b中,k的正负决定直线的升降;b的正负决定直线与y轴交点的位置是在y轴的正方向上还是负方向上.

练习册系列答案
相关题目
11.下列说法中,正确的个数有( )
①一条直线的平行线只有一条:
②过一点可以作一条直线与已知直线平行;
④过一点作直线的平行线仅有一条或不存在;
④过直线外一点有且只有一条直线与已知直线平行.
①一条直线的平行线只有一条:
②过一点可以作一条直线与已知直线平行;
④过一点作直线的平行线仅有一条或不存在;
④过直线外一点有且只有一条直线与已知直线平行.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.考虑下面两种宽带网的收费方式:
设月上网时间为xh.
(Ⅰ)用含有x的式子填写表格:
(Ⅱ)在某种上网时间下,两种收费方式能否相等?如果能,这时的上网时间是多少?如果不能,说明理由.
| 收费方式 | 月使用费(元) | 包时上网时间(h) | 超时费(元/min) |
| A | 30 | 25 | 0.05 |
| B | 50 | 50 | 0.05 |
(Ⅰ)用含有x的式子填写表格:
| 0≤x<25 | 25<x≤50 | x>50 | |
| 收费方式A应收取费用(元) | 30 | 3x-45 | 3x-45 |
| 收费方式B应收取费用(元) | 50 | 50 | 3x-100 |
10. 如图,正方形ABCD的四个顶点分别在四条平行线l1,l2,l3,l4上,AD,BC边分别与l2,l3相交于点F,E,这四条直线中相邻两条之间的距离依次为a,b,c(a>0,b>0,c>0),且AB边于直线l2的夹角为α,则下列结论错误的是( )
如图,正方形ABCD的四个顶点分别在四条平行线l1,l2,l3,l4上,AD,BC边分别与l2,l3相交于点F,E,这四条直线中相邻两条之间的距离依次为a,b,c(a>0,b>0,c>0),且AB边于直线l2的夹角为α,则下列结论错误的是( )
 如图,正方形ABCD的四个顶点分别在四条平行线l1,l2,l3,l4上,AD,BC边分别与l2,l3相交于点F,E,这四条直线中相邻两条之间的距离依次为a,b,c(a>0,b>0,c>0),且AB边于直线l2的夹角为α,则下列结论错误的是( )
如图,正方形ABCD的四个顶点分别在四条平行线l1,l2,l3,l4上,AD,BC边分别与l2,l3相交于点F,E,这四条直线中相邻两条之间的距离依次为a,b,c(a>0,b>0,c>0),且AB边于直线l2的夹角为α,则下列结论错误的是( )| A. | a=c | B. | 当a=b=c时,四边形BEDF是菱形 | ||
| C. | $\frac{AF}{AB}$=$\frac{a}{a+b}$ | D. | 正方形ABCD面积为(a+b)2+c2 |
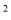 -3mx+6m=0的一个根,则m的值为( )
-3mx+6m=0的一个根,则m的值为( )
 1×
1× =1-
=1-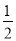
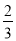 =2-
=2-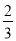
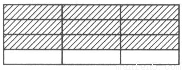
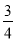 =3-
=3-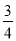

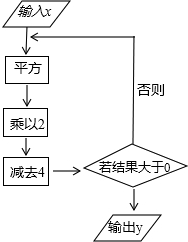 根据如图所示的程序计算.
根据如图所示的程序计算. 如图,已知在等腰直角三角形ABC中,∠CAB=90°,以AB为边向外作等边△ABD,AE⊥BD,CD、AE交于点M,若DM=1,求BC的值.
如图,已知在等腰直角三角形ABC中,∠CAB=90°,以AB为边向外作等边△ABD,AE⊥BD,CD、AE交于点M,若DM=1,求BC的值.