题目内容
x1、x2是一元二次方程x2-4x+k+1=0的两个根
（1）当k=0时，求5（x1+x2）-
的值
（2）是否存在整数k满足x1x2＞x1+x2-2，若有请求出k的值，若没有请说明理由．
解：（1）把k=0代入方程x2-4x+k+1=0，有
x2-4x+1=0，
∴x1+x2=-
=4，x1x2=
=1，
∴5（x1+x2）-=5×4-
=19；
（2）∵x1、x2是一元二次方程x2-4x+k+1=0的两个根，
∴x1+x2=-=4，x1x2==k+1，
又∵x1x2＞x1+x2-2，
∴k+1＞4-2，
解得k＞1．
分析：（1）先把k=0代入方程x2-4x+k+1=0中，得到一个方程：x2-4x+1=0，再根据根与系数的关系，可求出
x1+x2，x1x2的值，把它们代入5（x1+x2）-中计算即可；（2）先根据根与系数的关系，求出
x1+x2=-=4，x1x2==k+1，然后把x1+x2，x1x2的值代入不等式，得到关于k的不等式，解不等式即可．
点评：本题考查了根与系数的关系，在解不等式时一定要注意数值的正负与不等号的变化关系．
x2-4x+1=0，
∴x1+x2=-
=4，x1x2==1，∴5（x1+x2）-
=5×4-=19；（2）∵x1、x2是一元二次方程x2-4x+k+1=0的两个根，
∴x1+x2=-
=4，x1x2==k+1，又∵x1x2＞x1+x2-2，
∴k+1＞4-2，
解得k＞1．
分析：（1）先把k=0代入方程x2-4x+k+1=0中，得到一个方程：x2-4x+1=0，再根据根与系数的关系，可求出
x1+x2，x1x2的值，把它们代入5（x1+x2）-
中计算即可；（2）先根据根与系数的关系，求出x1+x2=-
=4，x1x2==k+1，然后把x1+x2，x1x2的值代入不等式，得到关于k的不等式，解不等式即可．点评：本题考查了根与系数的关系，在解不等式时一定要注意数值的正负与不等号的变化关系．
练习册系列答案
阅读快车系列答案
相关题目
小明在复习数学知识时，针对“求一元二次方程的解”，整理了以下的几种方法，请你按有关内容补充完整：
| 复习日记卡片 |
| 内容：一元二次方程解法归纳 时间：2007年6月×日 |
| 举例：求一元二次方程x2-x-1=0的两个解 |
| 方法一：选择合适的一种方法（公式法、配方法、分解因式法）求解 解方程：x2-x-1=0． 解： |
方法二：利用二次函数图象与坐标轴的交点求解如图所示，把方程x2-x-1=0的解看成是二次函数y=  |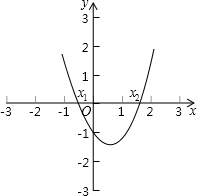
方法三：利用两个函数图象的交点求解 （1）把方程x2-x-1=0的解看成是一个二次函数y= （2）画出这两个函数的图象，用x1，x2在x轴上标出方程的解．  |
20、阅读材料，解答问题．
（2012•兰州）若x1、x2是关于一元二次方程ax2+bx+c（a≠0）的两个根，则方程的两个根x1、x2和系数a、b、c有如下关系：x1+x2=-