题目内容
(12分)如图,圈O1与圈O2相交于A、B两点,若AB=O1A=4,O2A= .
.

求:(1)∠O1AO2的度数;
(2)O1与O2之间的距离.
(1)105°;(2) .
.
【解析】
试题分析:(1)如图,作辅助线,由O1B=AB=O1A=4得到△ABO1为等边三角形,∠O1AB=α=60°;利用cos∠O2AB= =
= ,求出∠O2AB=β=45°,问题即可解决;
,求出∠O2AB=β=45°,问题即可解决;
(2)由sinα= ,sinβ=
,sinβ= ,分别求出
,分别求出 ,
, ,问题即可解决.
,问题即可解决.
试题解析:(1)如图,连接O1O2、O1B、O2B;则O1O2⊥AB、AC=BC=2;∵O1B=AB=O1A=4,∴△ABO1为等边三角形,∠O1AB=α=60°;在直角△ACO2中,∵cos∠O2AB= =
= ,∴∠O2AB=β=45°,∴∠O1AO2=60°+45°=105°;
,∴∠O2AB=β=45°,∴∠O1AO2=60°+45°=105°;
(2)∵sinα= ,sinβ=
,sinβ= ,∴
,∴ ,
, ,∴
,∴ .
.

考点:相交两圆的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若△ABC∽△A′B′C′,相似比为1:2,则△ABC与△A′B′C′的面积的比( )
| A.1:2 | B.2:1 | C.1:4 | D.4:1 |
 B.
B. C.
C. D.
D.



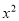 -m=2x有两个不相等的实数根,则m的取值范围是( )
-m=2x有两个不相等的实数根,则m的取值范围是( )