Question

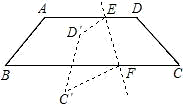如图，把一等腰梯形ABCD沿EF折叠后，点D、C分别落在D′、C′处，若∠AED'=20°，则∠EFB的度数等于

1. A.
   50°
2. B.
   60°
3. C.
   70°
4. D.
   80°

Answer 1

D
分析：根据等腰梯形的性质及翻折变换的性质可得到∠DEF的度数，再根据平行线的性质即可求出∠EFB的度数．
解答：由已知得∠DEF=∠D'EF．
又因为∠AED=180度，∠AED'=20°，所以∠DEF=80度．
又因为AD∥BC，所以∠EFB=∠DEF=80°．
点评：此题主要考查翻折变换和平行线的性质，得出∠DEF=∠D'EF是关键．