��Ŀ����
����Ŀ����ͼ����������ABCD�У���E��BC������ֱ����һ���㣨�����B��C�غϣ�������B��BF��DE��������DE�ڵ�F������CF��
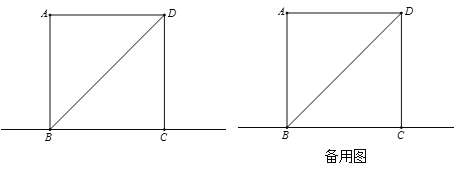
��1����ͼ������E���߶�BC��ʱ����BDF=����
�ٰ�Ҫ��ȫͼ�Σ�
�ڡ�EBF=______________���ú�����ʽ�ӱ�ʾ����
���ж��߶� BF��CF��DF֮���������ϵ����֤����
��2������E��ֱ��BC��ʱ��ֱ��д���߶�BF��CF��DF֮���������ϵ������֤����
���𰸡���1���ټ���������45��-�������߶�BF��CF��DF֮���������ϵ��![]() ��֤������������2��
��֤������������2��![]() ��
��![]() ��
��![]()
��������
(1)�������ⲹȫͼ�μ��ɣ�
���������ε����ʵó�![]() ���������ε�������ʵó�
���������ε�������ʵó�![]() ����ֱ�������ε����ʵó�
����ֱ�������ε����ʵó�![]() ���ɣ�
���ɣ�
����DF�Ͻ�ȡDM=BF������CM��֤����CDM�ա�CBF���ó�CM=CF����DCM=��BCF���ó�MF=![]() ���ɵó����ۣ�
���ɵó����ۣ�
(2)������������ٵ���E���߶�BC��ʱ��DF=BF+![]() ������ͬ(1)�ۣ�
������ͬ(1)�ۣ�
�ڵ���E���߶�BC���ӳ�����ʱ��BF=DF+![]() ����BF_�Ͻ�ȡBM=DF������CM.ͬ(1)�۵���CBM�ա�CDF�ó�CM=CF����BCM=��DCF��֤����CMF�ǵ���ֱ�������Σ��ó�MF=
����BF_�Ͻ�ȡBM=DF������CM.ͬ(1)�۵���CBM�ա�CDF�ó�CM=CF����BCM=��DCF��֤����CMF�ǵ���ֱ�������Σ��ó�MF=![]() �����ɵó����ۣ�
�����ɵó����ۣ�
�۵���E���߶�CB���ӳ�����ʱ��BF+DF=![]() ����DF�Ͻ�ȡDM=BF������CM��ͬ(1)�۵�:ACDM�ա�CBF�ó�CM=CF����DCM=��BCF��֤����CMF�ǵ���ֱ�������Σ��ó�MF=
����DF�Ͻ�ȡDM=BF������CM��ͬ(1)�۵�:ACDM�ա�CBF�ó�CM=CF����DCM=��BCF��֤����CMF�ǵ���ֱ�������Σ��ó�MF=![]() �����ɵó�����.
�����ɵó�����.
��1������ͼ��

�����ı���ABCD�������Σ�
���ABC=90����![]() ��
��
��![]() ��
��
��BF��DE,
���BFE=90����
��![]() ,
,
�ʴ�Ϊ��45��-����
���߶�BF��CF��DF֮���������ϵ��![]() .
.
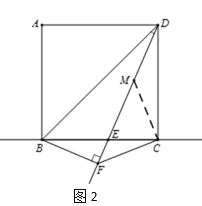
֤�����£���DF�Ͻ�ȡDM=BF������CM.��ͼ2��ʾ��
�� ������ABCD��
�� BC=CD����BDC=��DBC=45������BCD=90��
���CDM=��CBF=45��-����
���CDM�ա�CBF��SAS��.
�� DM=BF�� CM=CF����DCM=��BCF.
�� ��MCF =��BCF+��MCE
=��DCM+��MCE
=��BCD=90����
�� MF =![]() .
.
��![]()
��2�������������������E���߶�BC��ʱ��DF=BF+![]() ������ͬ(1)����
������ͬ(1)����
�ڵ���E���߶�BC���ӳ�����ʱ��BF=DF+![]() ���������£�
���������£�
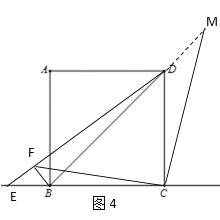
��BF�Ͻ�ȡBM=DF������CM����ͼ3��ʾ��
ͬ(1)�����ã���CBM�ա�CDF(SAS)��
��CM=CF����BCM=��DCF.
����MCF=��DCF+��MCD=��BCM+��MCD=��BCD=90����
����CMF�ǵ���ֱ�������Σ�
��MF=![]() ��
��
��BF=BM+MF=DF+![]() ��
��
�۵���E���߶�CB���ӳ�����ʱ��BF+DF=![]() ���������£�
���������£�
��DF�Ͻ�ȡDM=BF������CM����ͼ4��ʾ��
ͬ��1�����ã���CDM����CBF��
��CM=CF����DCM=��BCF��
���MCF=��DCF+��MCD=��DCF+��BCF=��BCD=90����
���CMF�ǵ���ֱ�������Σ�
��MF=![]() ,
,
��DM+DF=![]() ��
��
��BF+DF=![]() ;
;
��������������E��ֱ��BC��ʱ���߶�BF��CF��DF֮���������ϵΪ��![]() ����
����![]() ����
����![]() .
.


 ��У����ϵ�д�
��У����ϵ�д�