��Ŀ����
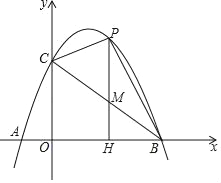
����Ŀ����ͼ����֪���κ���y��ax2+bx+c��ͼ����x���ཻ��A����1��0����B��3��0�����㣬��y���ཻ�ڵ�C��0��3��
��1����������κ����ı���ʽ��ֱ��д���������ꣻ
��2����P�ǵ�һ������������κ�����ͼ��������һ�㣬PH��x���ڵ�H����BC���ڵ�M������PC�����P�ĺ�����Ϊt
�����߶�PM�����ֵ��
��S��PBM��S��MHB��1��2ʱ����tֵ��
������PCM�ǵ���������ʱ��ֱ��д��P�����꣮
���𰸡���1����1��4����2����![]() ��
��![]() ������PCM�ǵ���������ʱ����P������Ϊ��2��3����3��
������PCM�ǵ���������ʱ����P������Ϊ��2��3����3��![]() ����2+4
����2+4![]() ����1��4����
����1��4����
��������
�躯������ʽΪy��ax2+bx+c����A����1��0����B��3��0����C��0��3�����뼴����
������ֱ��BC�ı���ʽ�������P�ĺ�����Ϊt��Ȼ��PM�ij���ʾ�ɺ�������ʽ������;
����S��PBM��S��MHB��1��2ת���ɵ�֮��MH��2PM��������P��M�����꣬�г���ʽ���������ֵ���پ����ɵã�
�����������PC=PM��PC=CM��PM=CM���t��ֵ���ټ��飬���ɵ�.
��1����A����1��0����B��3��0����C��0��3������y��ax2+bx+c���ã�
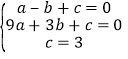 �����
�����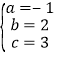 ��
��
����κ����ı���ʽΪy����x2+2x+3��
��y����x2+2x+3������x��1��2+4��
����κ���ͼ��Ķ�������Ϊ��1��4����
��2������ֱ��BC�ı���ʽΪy��mx+n��m��0����
��B��3��0����C��0��3������y��mx+n���ã�
![]() ����ã�
����ã�![]() ��
��
��ֱ��BC�ı���ʽΪy����x+3��
�ߵ�P�ĺ�����Ϊt��0��t��3����
���P��������t����t2+2t+3������M��������t����t+3����
��PM����t2+2t+3������t+3������t2+3t������t��![]() ��2+
��2+![]() ��
��
���߶�PM�����ֵΪ![]() ��
��
�ڡߵ�P������Ϊ��t����t2+2t+3������M������Ϊ��t����t+3����
���H��������t��0����
��PM����t2+2t+3������t+3������t2+3t��MH����t+3��
�ߡ�PBM����MHB�ȸߣ�S��PBM��S��MHB��1��2��
��MH��2PM������t+3����2t2+6t��
��ã�t1��![]() ��t2��3���������⣬��ȥ����
��t2��3���������⣬��ȥ����
�൱S��PBM��S��MHB��1��2ʱ��t��ֵΪ![]() ��
��
�ۡߵ�P������Ϊ��t����t2+2t+3������M������Ϊ��t����t+3������C������Ϊ��0��3����
��PM����t2+2t+3������t+3������t2+3t��CM��![]() ��PC��
��PC��![]() ��
��
��PM��PCʱ���Щ�t2+3t��![]() ��
��
��0��t��3��
��ԭ���̿�����Ϊ��2t��4��0��
��ã�t��2��
���P��������2��3����
��PM��CMʱ���Щ�t2+3t��![]() t��
t��
��ã�t1��0����ȥ����t2��3��![]() ��
��
���P��������3��![]() ����2+4
����2+4![]() ����
����
��CM��PCʱ����![]() t��
t��![]() ��
��
��0��t��3��
��ԭ���̿�����Ϊ��t2��4t+3��0��
��ã�t1��1��t2��3����ȥ����
���P��������1��4����
��������������PCM�ǵ���������ʱ����P������Ϊ��2��3����3��![]() ����2+4
����2+4![]() ����1��4����
����1��4����

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�