Question

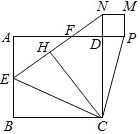
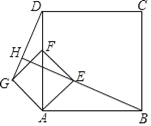
【题目】四边形ABCD、AEFG都是正方形，当正方形AEFG绕点A逆时针旋转45°时，如图，连接DG、BE，并延长BE交DG于点H，且BH⊥DG与H，若AB=4，AE=时，则线段BH的长是（　　）

A. B. 16C. D.

Answer 1

【答案】C

【解析】

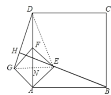
连结GE交AD于点N，连结DE，由于正方形AEFG绕点A逆时针旋转45°，AF与EG互相垂直平分，且AF在AD上，由AE=可得到AN=GN=1，所以DN=4-1=3，然后根据勾股定理可计算出DG=，则BE=，解着利用S△DEG=GEND=DGHE可计算出HE，所以BH=BE+HE．

连结GE交AD于点N，连结DE，如图，

∵正方形AEFG绕点A逆时针旋转，
∴AF与EG互相垂直平分，且AF在AD上，
∵AE=，
∴AN=GN=1，
∴DN=41=3，
在Rt△DNG中,DG==；
由题意可得：△ABE相当于逆时针旋转90得到△AGD，
∴DG=BE=，
∵S△DEG=GEND=DGHE，
∴HE==，
∴BH=BE+HE=+=.
故答案为C.