题目内容
 如图所示,三角形ABC的面积为1,E是AC的中点,O是BE的中点.连接AO,并延长交BC于D,连接CO并延长交AB于F.求四边形BDOF的面积.
如图所示,三角形ABC的面积为1,E是AC的中点,O是BE的中点.连接AO,并延长交BC于D,连接CO并延长交AB于F.求四边形BDOF的面积.
分析:分别求出三角形BOF和三角形BOD的面积,再计算四边形BDOF的面积.利用等高的两三角形面积之比等于底边之比列出方程.
解答:解:设S△BOF=x,S△BOD=y.
因为E是AC的中点,0是BE的中点,
且S△ABC=1
所以S△AOE=S△COE=S△AOB=S△COB=
则S△AOF=
-x,S△ACF=
-x,S△BCF =
+x.
得
=
即
-x2=
x- x2,得x=
.
又S△COD=
-y,S△ACD=
-y,S△ABD=
+y.
得
=
即
-y2=
y-y2
得y=
.
所以四边形BDOF的面积=x+y=
+
=
.
因为E是AC的中点,0是BE的中点,
且S△ABC=1
所以S△AOE=S△COE=S△AOB=S△COB=
| 1 |
| 4 |
则S△AOF=
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
得
| ||
| x |
| ||
|
即
| 1 |
| 16 |
| 3 |
| 4 |
| 1 |
| 12 |
又S△COD=
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
得
| y | ||
|
| ||
|
即
| 1 |
| 16 |
| 3 |
| 4 |
得y=
| 1 |
| 12 |
所以四边形BDOF的面积=x+y=
| 1 |
| 12 |
| 1 |
| 12 |
| 1 |
| 6 |
点评:考查了三角形面积的应用.解题关键在于找出等高的两三角形面积与底边的对应关系.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
 12、如图所示,三角形DEF平移得到三角形ABC,已知∠B=45°,∠C=65°,AB=2cm,则∠DFE=
12、如图所示,三角形DEF平移得到三角形ABC,已知∠B=45°,∠C=65°,AB=2cm,则∠DFE=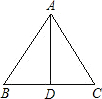 某建筑工地需制作如图所示的三角形支架.己知AB=AC=3m,BC=4m.俗话说“直木顶千斤”,为了增加该三角形支架的耐压程度,需加固一根中柱AD,求中柱AD的长.(精确到0.1m).
某建筑工地需制作如图所示的三角形支架.己知AB=AC=3m,BC=4m.俗话说“直木顶千斤”,为了增加该三角形支架的耐压程度,需加固一根中柱AD,求中柱AD的长.(精确到0.1m). 某市在“旧城改造”中计划在市内一块如图所示的三角形空地上种植某种草皮以美化环境,已知AC=30m,AB=20m,∠BAC=150°,这种每平方米的售价是a元,求购买这种草皮至少需要多少元?
某市在“旧城改造”中计划在市内一块如图所示的三角形空地上种植某种草皮以美化环境,已知AC=30m,AB=20m,∠BAC=150°,这种每平方米的售价是a元,求购买这种草皮至少需要多少元? (阅读理解题)如图所示,CE⊥AB于点E,BD⊥AC于点D,BD,CE交于点O,且AO平分∠BAC.
(阅读理解题)如图所示,CE⊥AB于点E,BD⊥AC于点D,BD,CE交于点O,且AO平分∠BAC. 如图所示,三角形ABO绕点O旋转得到三角形CDO,在这个旋转过程中:
如图所示,三角形ABO绕点O旋转得到三角形CDO,在这个旋转过程中: