题目内容
【题目】在![]() 中,
中,![]() 分别是边
分别是边![]() 上的点,
上的点,![]() 和
和![]() 交于点
交于点![]() ,且
,且![]() .
.
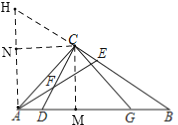
(1)如图![]() ,求证:
,求证:![]() ;
;
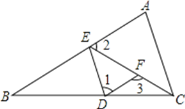
(2)如图![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]()
![]() ,求证
,求证![]() ;
;
(3)如图![]() ,在(2)的条件下,
,在(2)的条件下,![]() ,求线段
,求线段![]() 的长.
的长.

【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)根据三角形内角和定理可得∠ECF+∠CFE+∠CEF=180°,![]() ,由
,由![]() 且
且![]() 是公共角即可证明
是公共角即可证明![]() (2)根据锐角互余的关系可得
(2)根据锐角互余的关系可得![]() ,根据
,根据![]() 及外角性质可得∠CAB=∠CGA,进而可得AC=CG;(3)过点
及外角性质可得∠CAB=∠CGA,进而可得AC=CG;(3)过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 分别作
分别作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,根据等腰直角三角形的性质可得
,根据等腰直角三角形的性质可得![]() 进而可得AG=2MC,由∠HAB=90°,∠CAB=45°可得
进而可得AG=2MC,由∠HAB=90°,∠CAB=45°可得![]() 平分
平分![]() ,由
,由![]() 可得CM=CN,根据四边形内角和及平角的定义可得
可得CM=CN,根据四边形内角和及平角的定义可得![]() ,利用AAS可证明△HNC≌△CMD,即可证明CD=CH,根据已知即可证明AE=HE,根据(1)得
,利用AAS可证明△HNC≌△CMD,即可证明CD=CH,根据已知即可证明AE=HE,根据(1)得![]() ,由
,由![]() 可得∠AEC=∠H,可得AE=AH,进而可得
可得∠AEC=∠H,可得AE=AH,进而可得![]() ,在
,在![]() 中,
中,![]() 可得∠B=30°,根据含30°角的直角三角形性质可知
可得∠B=30°,根据含30°角的直角三角形性质可知![]() ,根据面积公式可得
,根据面积公式可得![]() ,即可求出CM的值,进而根据
,即可求出CM的值,进而根据![]() 可得BC的长.
可得BC的长.
(1)在![]() 中,∠ECF+∠CFE+∠CEF=180°,
中,∠ECF+∠CFE+∠CEF=180°,
在![]() 中,
中,![]()
![]() 且
且![]() 是公共角
是公共角
∴∠CEF=∠CDB
即![]()
(2)![]() ,
,
∴∠DCB=∠ACG=90°,
∴![]()
即![]()
∵∠ACD+∠B=∠CAB,
∴∠GCB+∠B=∠CAB,
∵∠CGA=∠GCB+∠B,
∴∠CAB=∠CGA,
∴AC=GC
(3)如图,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 分别作
分别作![]() 于点
于点![]() ,
,![]() 于点
于点![]()
![]() 且
且![]()
∴∠CAG=∠CGA=45°,![]() ,
,
∴![]() ,
,
∴![]()
∴![]()
∵![]()
∴![]() ,
,
∵∠CAG=45°,
∴∠CAH=∠CAG,
![]() 平分
平分![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在四边形![]() 中,
中,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴AE=AH,
∵![]() ,CM=CN,∠HNC=∠CMD,
,CM=CN,∠HNC=∠CMD,
∴△HNC≌△CMD,
∴CD=CH,
∵CE+CD=AE,
∴CE+CH=AE=EH
∴AE=EH=HA,
∴∠H=60°,
在![]() 中,
中,![]()
∴∠B=30°,
在![]() 中,
中,![]()
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.