题目内容
已知:如图,在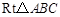 中,
中,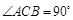 ,
,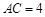 ,
,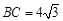 ,以
,以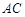 为直径的⊙O交
为直径的⊙O交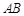 于点
于点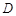 ,点
,点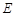 是
是 的中点,OB,DE相交于点F。
的中点,OB,DE相交于点F。
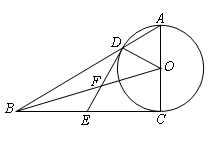
小题1:(1)求证: 是⊙O的切线;
是⊙O的切线;
小题2:(2)求EF:FD的值。
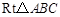 中,
中,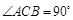 ,
,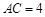 ,
,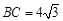 ,以
,以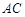 为直径的⊙O交
为直径的⊙O交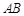 于点
于点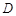 ,点
,点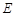 是
是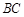 的中点,OB,DE相交于点F。
的中点,OB,DE相交于点F。
小题1:(1)求证:
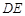 是⊙O的切线;
是⊙O的切线;小题2:(2)求EF:FD的值。
小题1:(1)证明:连结
 (如图), …………………… 1分
(如图), …………………… 1分∵AC是⊙O的直径,
∴
 。
。  是
是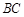 的中点,
的中点, 。
。∴

 ,
,  。
。 ,
, 。
。 。
。即
 。
。∵点D在⊙O上,
∴
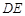 是⊙O的切线 。 ………………………………… 3分
是⊙O的切线 。 ………………………………… 3分
小题2:(2)解:连结OE。
∵E是BC的中点,O是AC的中点,
∴OE∥AB,OE=
 AB。
AB。∴△OEF∽△BDF。
在
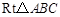 中,AC = 4,
中,AC = 4, ,
,根据勾股定理,得 AB= 8,
∴OE= 4,
∵sin∠ABC=
 ,
,∴∠ABC=30°。
∴∠A=60°。
∴
 是边长为2的等边三角形。
是边长为2的等边三角形。∴
 ,BD= AB-AD=6。
,BD= AB-AD=6。∴EF:FD=OE:BD = 4:6=2:3 。 …… 5分
略

练习册系列答案
相关题目
 、
、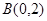 ,如果点
,如果点 在
在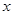 轴上(
轴上( 不重合),当点
不重合),当点 组成的三角形与
组成的三角形与 相似(至少找出两个满足条件的点的坐标).
相似(至少找出两个满足条件的点的坐标).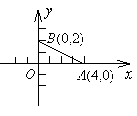
 是⊙O的直径,
是⊙O的直径, 是弦,过点
是弦,过点 作OD⊥AC于
作OD⊥AC于 ,连结
,连结 .
.
 ;
; ,求∠
,求∠ 的度数.
的度数. 的中位线,则
的中位线,则 与
与
 (x, y, z均不为0),则
(x, y, z均不为0),则 的值为 .
的值为 . ,点D、E在BC边上(均不与点B、C重合,点D始终在点E左侧),且∠DAE=45°.
,点D、E在BC边上(均不与点B、C重合,点D始终在点E左侧),且∠DAE=45°. 变量n的取值范围;
变量n的取值范围;
 中,
中,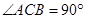 ,
,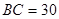 ,
,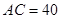 ,点P是AB边上任意一点,直线PE⊥AB,与边AC或BC相交于点E.点M在线段AP上,点N在线段BP上,且PM=PN,
,点P是AB边上任意一点,直线PE⊥AB,与边AC或BC相交于点E.点M在线段AP上,点N在线段BP上,且PM=PN,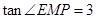 .
.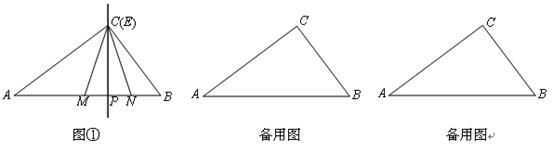
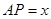 ,△ENB的面积为y,求y与x的函数关系式,并求出当x取何值时,y有最大值,最大值是多少?
,△ENB的面积为y,求y与x的函数关系式,并求出当x取何值时,y有最大值,最大值是多少?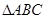 和
和 是绕点
是绕点 旋转的两个相似三角形,其中
旋转的两个相似三角形,其中 与
与 、
、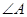 与
与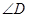 为对应角.
为对应角.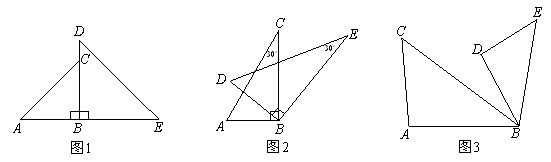
 、
、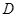 在同一条直线上的位置时,请直接写出线段
在同一条直线上的位置时,请直接写出线段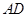 与线段
与线段 的关系;
的关系; 角的直角三角形,且两个三角形旋转到如图2的位置时,试确定线段
角的直角三角形,且两个三角形旋转到如图2的位置时,试确定线段 =
= ,
,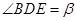 ,在绕点
,在绕点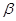 的式子表示夹角的度数;若改变,请说明理由.
的式子表示夹角的度数;若改变,请说明理由.