题目内容
 填空并完成以下证明:
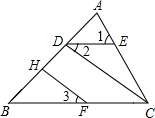
填空并完成以下证明:已知,如图,∠1=∠ACB,∠2=∠3,FH⊥AB于H,求证:CD⊥AB.
证明:∵∠1=∠ACB(已知)∴DE∥BC
∴∠2=
∵∠2=∠3(已知)∴∠3=
∴CD∥FH
∴∠BDC=∠BHF
又∵FH⊥AB(已知)
∴
考点:平行线的判定与性质,垂线
专题:推理填空题
分析:根据同位角相等,两直线平行由∠1=∠ACB得到DE∥BC,在根据平行线的性质得∠2=∠BCD,由于∠2=∠3,则∠3=∠BCD,于是根据平行线的判定得到CD∥FH,则根据平行线的性质得∠BDC=∠BHF,然后利用FH⊥AB得到CD⊥AB.
解答:证明:∵∠1=∠ACB(已知),
∴DE∥BC(同位角相等,两直线平行),
∴∠2=∠BCD,
∵∠2=∠3(已知),
∴∠3=∠BCD,
∴CD∥FH(同位角相等,两直线平行),
∴∠BDC=∠BHF(两直线平行,同位角相等)
又∵FH⊥AB(已知)
∴CD⊥AB.
故答案为同位角相等,两直线平行;∠BCD;∠BCD;同位角相等,两直线平行;两直线平行,同位角相等;
∴DE∥BC(同位角相等,两直线平行),
∴∠2=∠BCD,
∵∠2=∠3(已知),
∴∠3=∠BCD,
∴CD∥FH(同位角相等,两直线平行),
∴∠BDC=∠BHF(两直线平行,同位角相等)
又∵FH⊥AB(已知)
∴CD⊥AB.
故答案为同位角相等,两直线平行;∠BCD;∠BCD;同位角相等,两直线平行;两直线平行,同位角相等;
点评:本题考查了平行线的判定与性质:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行;两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.

练习册系列答案
相关题目
一个两位数的十位数字与个位数字的和是7,把这个两位数加上45后,结果恰好成为数字对调后组成的两位数,则这个两位数是( )
| A、25 | B、16 | C、34 | D、61 |
下面四个数中是负数的为( )
| A、0 | ||
| B、3 | ||
| C、-1.2 | ||
D、
|
 如图,已知四边形ABCD中,∠A=∠C,∠B=∠D,求证:四边形ABCD是平行四边形.
如图,已知四边形ABCD中,∠A=∠C,∠B=∠D,求证:四边形ABCD是平行四边形.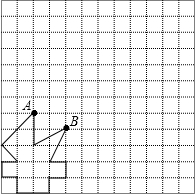 为迎接2014年8月16号在南京举行的青奥会,江都体育迷小强利用网格设计了一个“火炬”图案,请你帮帮他:
为迎接2014年8月16号在南京举行的青奥会,江都体育迷小强利用网格设计了一个“火炬”图案,请你帮帮他: 如图,已知△ABC和过点O的直线L.
如图,已知△ABC和过点O的直线L.