题目内容
在△ABC中,∠BAC=50°,若O是△ABC的外心,∠BOC=
100°
100°
;若O是内心,则∠BOC=115°
115°
.分析:已知了点O是△ABC的外心,那么∠A、∠BOC即为同弧所对的圆周角和圆心角,根据圆周角定理即可得到∠BOC的度数;利用内心的定义,OB,OC都是角平分线,因此可求出∠OBC与∠OCB的和,从而得到∠BOC的度数.
解答:解:由于点O是△ABC的外心,所以在△ABC的外接圆⊙O中,
∠BAC、∠BOC同对着弧BC;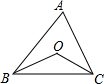
由圆周角定理得:∠BOC=2∠BAC=100°,
故答案为:100°;
∵O是△ABC的内心,
∴OB,OC分别平分∠ABC,∠ACB,
∴∠OBC+∠OCB=
=65°,
∴∠BOC=180°-65°=115°.
故答案为:115°.
∠BAC、∠BOC同对着弧BC;

由圆周角定理得:∠BOC=2∠BAC=100°,
故答案为:100°;
∵O是△ABC的内心,
∴OB,OC分别平分∠ABC,∠ACB,
∴∠OBC+∠OCB=
| 180°-50° |
| 2 |
∴∠BOC=180°-65°=115°.
故答案为:115°.
点评:此题主要考查了三角形的外接圆以及圆周角定理的相关知识和理解三角形内心的定义,记住三角形内角和定理是解题的关键.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 ;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x.
;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x.
 如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.
如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.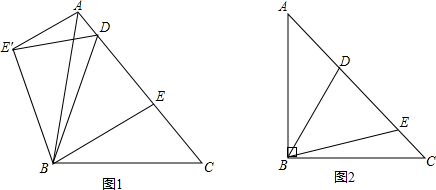
 如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以每秒4cm,的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.
如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以每秒4cm,的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.