题目内容
9.若关于x的一元二次方程2x2-2x+3m-1=0有两个实数根x1、x2,且x1x2>x1+x2-4,则实数m的取值范围是( )| A. | m>-$\frac{5}{3}$ | B. | m≤$\frac{1}{2}$ | C. | m<-$\frac{5}{3}$ | D. | -$\frac{5}{3}$<m≤$\frac{1}{2}$ |
分析 先利用判别式的意义得到m≤$\frac{1}{2}$,再根据根与系数的关系,由x1x2>x1+x2-4得到$\frac{3m-1}{2}$>1-4,此时解得m>-$\frac{5}{3}$,然后写出满足条件的m的取值范围.
解答 解:根据题意得△=(-2)2-4×2×(3m-1)≥0,解得m≤$\frac{1}{2}$,
∵x1+x2=1,x1x2=$\frac{3m-1}{2}$,
而x1x2>x1+x2-4,
∴$\frac{3m-1}{2}$>1-4,解得m>-$\frac{5}{3}$,
∴m的取值范围为-$\frac{5}{3}$<m≤$\frac{1}{2}$.
故选D.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了根的判别式.

练习册系列答案
相关题目
4.-( $\frac{1}{2}$-$\frac{1}{3}$)的相反数是( )
| A. | -$\frac{1}{2}$-$\frac{1}{3}$ | B. | -$\frac{1}{2}$+$\frac{1}{3}$ | C. | $\frac{1}{2}$-$\frac{1}{3}$ | D. | $\frac{1}{2}$+$\frac{1}{3}$ |
 B.
B. 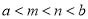
 D.
D. 
 小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图请你根据图中的信息,若小明把n个纸杯整齐叠放在一起时,它的高度h与n的函数关系是h=n+6.
小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图请你根据图中的信息,若小明把n个纸杯整齐叠放在一起时,它的高度h与n的函数关系是h=n+6. 如图,在平面直角坐标系中,直线y=$\frac{3}{4}$x-$\frac{3}{2}$与抛物线y=-$\frac{1}{4}$x2+bx+c交于A、B两点,点A在x轴上,点B的横坐标为-8.
如图,在平面直角坐标系中,直线y=$\frac{3}{4}$x-$\frac{3}{2}$与抛物线y=-$\frac{1}{4}$x2+bx+c交于A、B两点,点A在x轴上,点B的横坐标为-8. 如图,在⊙O中,弦AB、CD相交于点M,连接BC、AD,∠AMD=100°,∠A=30°,则∠B=50°.
如图,在⊙O中,弦AB、CD相交于点M,连接BC、AD,∠AMD=100°,∠A=30°,则∠B=50°.