题目内容
 直角坐标系xOy中,O是坐标原点,抛物线y=x2-x-6与x轴交于A,B两点(点A在点B左侧),与y轴交于点C.如果点M在y轴右侧的抛物线上,S△AMO=S△COB,那么点M的坐标是
直角坐标系xOy中,O是坐标原点,抛物线y=x2-x-6与x轴交于A,B两点(点A在点B左侧),与y轴交于点C.如果点M在y轴右侧的抛物线上,S△AMO=S△COB,那么点M的坐标是分析:根据解析式,易得A、B、C的坐标,因此S△COB可知,设点M的纵坐标为y,必有
×AO•|y|=S△COB,列方程即可解答y,然后代入直线解析式即可.
| 1 |
| 2 |
解答:解:在抛物线y=x2-x-6中,
当y=0时,x=-2或3,
即A(-2,0),B(3,0);
当x=0时,y=-6,
即C(0,-6);
故S△COB=9,
设点M的纵坐标为y,必有
×AO•|y|=9,
解可得y=±9,
将其代入解析式可得x的值为
,
(舍去),
故点M的坐标是(
,9).
当y=0时,x=-2或3,
即A(-2,0),B(3,0);
当x=0时,y=-6,
即C(0,-6);
故S△COB=9,
设点M的纵坐标为y,必有
| 1 |
| 2 |
解可得y=±9,
将其代入解析式可得x的值为
1+
| ||
| 2 |
1-
| ||
| 2 |
故点M的坐标是(
1+
| ||
| 2 |
点评:本题考查二次函数的有关性质,涉及图象与点的坐标的求法.

练习册系列答案
相关题目
 22、如图,已知△ABC的三个顶点A、B、C的坐标分别是A(3,4),B(-2,1),C(1,-2).
22、如图,已知△ABC的三个顶点A、B、C的坐标分别是A(3,4),B(-2,1),C(1,-2).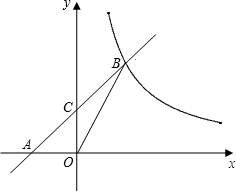 C(0,2),与反比例函数在第一象限内的图象交于点B(2,n),连接BO,若S△AOB=4.
C(0,2),与反比例函数在第一象限内的图象交于点B(2,n),连接BO,若S△AOB=4. 已知,如图,在平面直角坐标系xOy中,直线AB与x、y轴分别交于点A(
已知,如图,在平面直角坐标系xOy中,直线AB与x、y轴分别交于点A(