题目内容
某拱形门建筑的形状是抛物线，若取拱形门地面上两点的连线为x轴，它可以近似的用函数
表示（单位：m）．
（1）求拱形门的宽（地面上的两点之间的距离）；
（2）求拱形门的高．
解：（1）当y=0时，-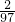
x2+4x=0，
解得：x1=0，x2=194；
则拱形门的宽为194m；
（2）∵抛物线y=-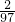x2+4x=-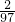（x-97）2+194，
∴拱形门的高为194m．
分析：（1）先求出当y=0时x的值，再根据x轴上两点间的距离公式就可以求出拱形门的宽．
（2）先求出抛物线的顶点坐标，即可得出拱形门的高．
点评：此题考查了二次函数的应用，用到的知识点是二次函数的顶点坐标和与x轴的交点，关键是把实际问题转化成数学问题．
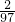x2+4x=0，解得：x1=0，x2=194；
则拱形门的宽为194m；
（2）∵抛物线y=-
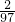x2+4x=-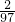（x-97）2+194，∴拱形门的高为194m．
分析：（1）先求出当y=0时x的值，再根据x轴上两点间的距离公式就可以求出拱形门的宽．
（2）先求出抛物线的顶点坐标，即可得出拱形门的高．
点评：此题考查了二次函数的应用，用到的知识点是二次函数的顶点坐标和与x轴的交点，关键是把实际问题转化成数学问题．
练习册系列答案
相关题目
如图，某拱形门建筑的形状是抛物线．若取拱形门地面上两点的连线为x轴，它可以近似地用函数
如图，某拱形门建筑的形状是抛物线．若取拱形门地面上两点的连线为x轴，它可以近似地用函数
表示（单位：m）．则拱形门的宽度大约是________m．