题目内容
如图,四边形OABC是菱形,点C在x轴上,AB交y轴于点H,AC交y轴于点M.点P从点A出发,以2单位长/秒的速度沿折线A-B-C运动,到达点C终止.已知点A(-3,4),设 点P的运动时间为t(秒),△PMB的面积为S(平方单位).
点P的运动时间为t(秒),△PMB的面积为S(平方单位).
(1)求点C和点B的坐标;
(2)求点M的坐标;
(3)求S与t的函数关系式;
(4)求S的最大值.
解:(1)∵A(-3,4),
∴AH=3,OH=4,
由勾股定理得:AO= =5,
=5,
∵菱形OABC,
∴OA=OC=BC=AB=5,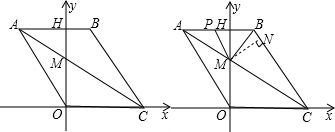
∴BH=AB-AH=5-3=2,
∴B(2,4),C(5,0).
(2)设直线AC的解析式是y=kx+b,
把A(-3,4),C(5,0)代入得:
 ,
,
解得: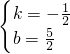
∴直线AC的解析式为 y=- x+
x+ ,
,
当x=0时,y=2.5
∴M(0,2.5).
(3)过M作MN⊥BC于N,
∵菱形OABC,
∴∠BAC=∠OCA,
∵MO⊥CO,MN⊥BC,
∴OM=MN,
当0≤t<2.5时,P在AB上,MH=4-2.5= ,
,
S= ×BP×MH=
×BP×MH= ×(5-2t)×
×(5-2t)× =-
=- t+
t+ ,
,
∴S=- t+
t+ ,
,
当2.5<t≤5时,P在BC上,S= ×PB×MN=
×PB×MN= ×(2t-5)×
×(2t-5)× =
= t-
t- ,
,
∴S= t-
t- ,
,
答:S与t的函数关系式是 S=- t+
t+ (0≤t<2.5)或 S=
(0≤t<2.5)或 S= t-
t- (2.5<t≤5).
(2.5<t≤5).
(4)当P在AB上时,高MH一定,只有BP取最大值即可,即P与A重合,S最大是 ×5×
×5× =
= ,
,
同理在BC上时,P与C重合时,S最大是 ×5×
×5× =
= ,
,
∴S的最大值是 ,
,
答:S的最大值是 .
.
分析:(1)根据A的坐标求出AH、OH,根据勾股定理求出AO,再利用菱形的性质即可求出点C和点B的坐标;
(2)由(1)可知点C和点B的坐标,设直线AC的解析式是y=kx+b,把A(-3,4),C(5,0)代入得到方程组,求出即可;
(3)过M作MN⊥BC于N,根据角平分线性质求出MN,P在AB上,根据三角形面积公式求出即可;P在BC上,根据三角形面积公式求出即可;
(4)求出P在AB的最大值和P在BC上的最大值比较即可得到答案.
点评:本题主要考查对勾股定理,三角形的面积,菱形的性质,角平分线性质,解二元一次方程组,用待定系数法求一次函数的解析式等知识点的理解和掌握,综合运用这些性质进行计算是解此题的关键.
∴AH=3,OH=4,
由勾股定理得:AO=
 =5,
=5,∵菱形OABC,
∴OA=OC=BC=AB=5,

∴BH=AB-AH=5-3=2,
∴B(2,4),C(5,0).
(2)设直线AC的解析式是y=kx+b,
把A(-3,4),C(5,0)代入得:
 ,
,解得:
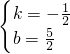
∴直线AC的解析式为 y=-
 x+
x+ ,
,当x=0时,y=2.5
∴M(0,2.5).
(3)过M作MN⊥BC于N,
∵菱形OABC,
∴∠BAC=∠OCA,
∵MO⊥CO,MN⊥BC,
∴OM=MN,
当0≤t<2.5时,P在AB上,MH=4-2.5=
 ,
,S=
 ×BP×MH=
×BP×MH= ×(5-2t)×
×(5-2t)× =-
=- t+
t+ ,
,∴S=-
 t+
t+ ,
,当2.5<t≤5时,P在BC上,S=
 ×PB×MN=
×PB×MN= ×(2t-5)×
×(2t-5)× =
= t-
t- ,
,∴S=
 t-
t- ,
,答:S与t的函数关系式是 S=-
 t+
t+ (0≤t<2.5)或 S=
(0≤t<2.5)或 S= t-
t- (2.5<t≤5).
(2.5<t≤5).(4)当P在AB上时,高MH一定,只有BP取最大值即可,即P与A重合,S最大是
 ×5×
×5× =
= ,
,同理在BC上时,P与C重合时,S最大是
 ×5×
×5× =
= ,
,∴S的最大值是
 ,
,答:S的最大值是
 .
.分析:(1)根据A的坐标求出AH、OH,根据勾股定理求出AO,再利用菱形的性质即可求出点C和点B的坐标;
(2)由(1)可知点C和点B的坐标,设直线AC的解析式是y=kx+b,把A(-3,4),C(5,0)代入得到方程组,求出即可;
(3)过M作MN⊥BC于N,根据角平分线性质求出MN,P在AB上,根据三角形面积公式求出即可;P在BC上,根据三角形面积公式求出即可;
(4)求出P在AB的最大值和P在BC上的最大值比较即可得到答案.
点评:本题主要考查对勾股定理,三角形的面积,菱形的性质,角平分线性质,解二元一次方程组,用待定系数法求一次函数的解析式等知识点的理解和掌握,综合运用这些性质进行计算是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 动.过点N作NP⊥OA于点P,连接AC交NP于Q,连接MQ.
动.过点N作NP⊥OA于点P,连接AC交NP于Q,连接MQ.  在MN上,并与MN上的点G重合,折痕为EF,点F为折痕与y轴的交点.
在MN上,并与MN上的点G重合,折痕为EF,点F为折痕与y轴的交点.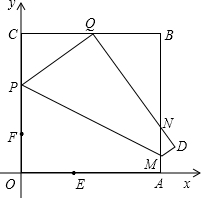
 (2012•呼伦贝尔)如图,四边形OABC是边长为2的正方形,反比例函数
(2012•呼伦贝尔)如图,四边形OABC是边长为2的正方形,反比例函数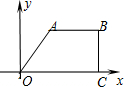 是( )
是( )