题目内容
如图,在△ABC中,D是边AC上一点,且BD=BC,点E、F分别是DC、AB的中点.求证:
(1)EF= AB;
AB;
(2)过A点作AG∥EF,交BE的延长线于点G,则BE=GE.
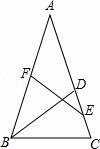
(1)证明:如图,连接BE,
∵BD=BC,点E是CD的中点,
∴BE⊥AC,
∵点F是AB的中点,
∴EF= AB;
AB;
(2)解:∵AF=EF= AB,
AB,
∴∠AEF=∠EAF,
∵AG∥EF,
∴∠AEF=∠EAG,
∴∠EAF=∠EAG,
又∵BE⊥AC,
∴BE=GE(等腰三角形三线合一).

点

练习册系列答案
相关题目
 =( )÷( )=
=( )÷( )= =
= =( )(填小数)
=( )(填小数) ﹣
﹣ +
+ ;
; 整数解共有2个,则m的取值范围是( )
整数解共有2个,则m的取值范围是( ) )求甲从B地返回A地的过程中,y与x之间的函数关系式,并写出自变量x的取值范围;
)求甲从B地返回A地的过程中,y与x之间的函数关系式,并写出自变量x的取值范围;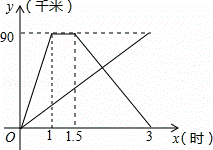
 x+4的图象与x轴、y轴分别交于A,B两点,则线段AB的长为
x+4的图象与x轴、y轴分别交于A,B两点,则线段AB的长为