题目内容
如图所示,AB是⊙O的直径,OD⊥弦BC于点F,且交⊙O于点E,若∠AEC=∠ODB.
(1)判断直线BD和⊙O的位置关系,并给出证明;
(2)当AB=10,BC=8时,求BD的长.
(1)答:BD和⊙O相切.
证明:∵OD⊥BC,
∴∠OFB=∠BFD =90°,
∴∠D+∠3=90°.
∵∠4=∠D=∠2, ……………………………1分
∴∠2+∠3=90°,
∴∠OBD=90°,
即OB⊥BD.
∵点B在⊙O上,
∴BD和⊙O相切. ……………………………2分
(2) ∵OD⊥BC,BC=8,
∴BF=FC=4. ……………………………3分
∵ AB=10,
∴OB=OA=5.
在Rt△OFB中, ∠OFB =90°,
∵OB=5,BF=4,
∴OF=3. ……………………………4分
∴tan∠1=![]() .
.
在Rt△OBD中, ∠OBD =90°,
∵tan∠1= , OB=5,
, OB=5,
∴![]() . …………………………… 5分
. …………………………… 5分
解析:略

练习册系列答案
相关题目
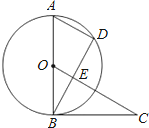 如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A.
如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A.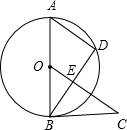 如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A,OC⊥BD于点E.
如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A,OC⊥BD于点E.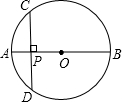 如图所示,AB是⊙O的直径,弦CD⊥AB于点P,CD=10cm,AP:PB=1:5,则⊙O的半径为
如图所示,AB是⊙O的直径,弦CD⊥AB于点P,CD=10cm,AP:PB=1:5,则⊙O的半径为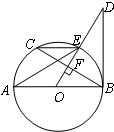 如图所示,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,且∠AEC=∠ODB.
如图所示,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,且∠AEC=∠ODB. 如图所示,AB是⊙O直径,∠D=35°,则∠BOC等于( )
如图所示,AB是⊙O直径,∠D=35°,则∠BOC等于( )