题目内容
已知ax2+bx+1与2x2-3x+1的积不含x3和x项,试计算下面代数式的值. .
.
解:(ax2+bx+1)•(2x2-3x+1),
=2ax4-3ax3+ax2+2bx3-3bx2+bx+2x2-3x+1,
=2ax4+(-3a+2b)x3+(a-3b+2)x2+(b-3)x+1,
∵不含x3和x项,
∴b-3=0,-3a+2b=0,
∴b=3,a=2,
把a=2,b=3代入得:

= +
+ +
+ +
+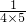 +…+
+…+
= -
- +
+ -
- +
+ -
- +
+ -
- +…+
+…+ -
-
=1-
=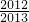 .
.
分析:首先计算出ax2+bx+1与2x2-3x+1的积,再根据不含x3和x项求出a,b的值,然后把a,b的值代入 中可解得答案.
中可解得答案.
点评:此题主要考查了多项式乘以多项式以及分式的求值,解决此题关键是求出a,b的值.
=2ax4-3ax3+ax2+2bx3-3bx2+bx+2x2-3x+1,
=2ax4+(-3a+2b)x3+(a-3b+2)x2+(b-3)x+1,
∵不含x3和x项,
∴b-3=0,-3a+2b=0,
∴b=3,a=2,
把a=2,b=3代入得:

=
 +
+ +
+ +
+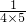 +…+
+…+
=
 -
- +
+ -
- +
+ -
- +
+ -
- +…+
+…+ -
-
=1-

=
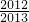 .
.分析:首先计算出ax2+bx+1与2x2-3x+1的积,再根据不含x3和x项求出a,b的值,然后把a,b的值代入
 中可解得答案.
中可解得答案.点评:此题主要考查了多项式乘以多项式以及分式的求值,解决此题关键是求出a,b的值.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目