题目内容
8.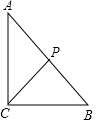 如图,△ABC中,∠ACB=90°,BC=6cm,AC=8cm,动点P从△ABC的顶点A出发,以2cm/s的速度向B点运动,连接CP,设点P的运动时间为t(单位:s),则当t的时间为2或2.5或1.4时,△BCP为等腰三角形.
如图,△ABC中,∠ACB=90°,BC=6cm,AC=8cm,动点P从△ABC的顶点A出发,以2cm/s的速度向B点运动,连接CP,设点P的运动时间为t(单位:s),则当t的时间为2或2.5或1.4时,△BCP为等腰三角形.
分析 根据∠ACB=90°,BC=6cm,AC=8cm,利用勾股定理求出AB的长,①BP=BC、②PC=PB、③BC=PC分别求解可得.
解答 解:∵△ABC中,∠ACB=90°,BC=6cm,AC=8cm,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{8}^{2}+{6}^{2}}$=10(cm),
①当BP=BC=6cm时,
∴AP=AB-BP=10-6=4,
∵动点P从A出发,以2cm/s的速度沿AB移动,4÷2=2,
∴点P出发2s时,△BCP为等腰三角形;
②当PC=PB时,P为斜边AB的中点,
此时AP=BP=PC=5cm,5÷2=2.5,
∴点P出发2.5s时,△BCP为等腰三角形;
③当BC=PC时,过点C作CD⊥AB于点D,如图所示:
则△BCD∽△BAC,
∴$\frac{BC}{BA}$=$\frac{BD}{BC}$,即$\frac{6}{10}$=$\frac{BD}{6}$,
解得:BD=3.6,
∴BP=2BD=7.2,
∴AP=10-7.2=2.8,2.8÷2=1.4,
∴点P出发1.4s时,△BCP为等腰三角形,
故当t的时间为2或2.5或1.4时,△BCP为等腰三角形;
故答案为:2或2.5或1.4.
点评 此题主要考查勾股定理和等腰三角形的判定,解答此题的关键是首先根据勾股定理求出AB的长,然后再利用等腰三角形的性质去判定.

练习册系列答案
相关题目
19.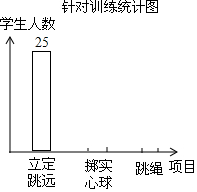 中考体考临近,某校计划让九年级10个班的480名学生在“立定跳远”、“掷实心球”、“跳绳”三个项目中选择一项进行针对性强化训练.为了提前了解全年级总体情况,小明从每个班中随机抽取5名学生进行问卷调查,并将统计结果制成如下两幅不完整的统计表和统计图.
中考体考临近,某校计划让九年级10个班的480名学生在“立定跳远”、“掷实心球”、“跳绳”三个项目中选择一项进行针对性强化训练.为了提前了解全年级总体情况,小明从每个班中随机抽取5名学生进行问卷调查,并将统计结果制成如下两幅不完整的统计表和统计图.
针对性训练统计表
(1)请将统计表、统计图补充完整;
(2)请以小明的统计结果来估算该校九年级480名学生参加“跳绳”训练的人数.
 中考体考临近,某校计划让九年级10个班的480名学生在“立定跳远”、“掷实心球”、“跳绳”三个项目中选择一项进行针对性强化训练.为了提前了解全年级总体情况,小明从每个班中随机抽取5名学生进行问卷调查,并将统计结果制成如下两幅不完整的统计表和统计图.
中考体考临近,某校计划让九年级10个班的480名学生在“立定跳远”、“掷实心球”、“跳绳”三个项目中选择一项进行针对性强化训练.为了提前了解全年级总体情况,小明从每个班中随机抽取5名学生进行问卷调查,并将统计结果制成如下两幅不完整的统计表和统计图.针对性训练统计表
| 项目 | 频数 | 百分比 |
| 立定跳远 | 25 | |
| 掷实心球 | 20% | |
| 跳绳 | ||
| 合计 | 50 | 1 |
(2)请以小明的统计结果来估算该校九年级480名学生参加“跳绳”训练的人数.
 如图,一棵树高9米,被大风刮断,树尖着地点B距树底部C为3米,求折断点A离地高度多少米?
如图,一棵树高9米,被大风刮断,树尖着地点B距树底部C为3米,求折断点A离地高度多少米?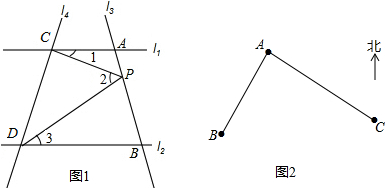
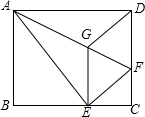 如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG. 如图,BC⊥AB,DE⊥AB,DF∥BG,由此可判断∠1=∠2,请说明理由.
如图,BC⊥AB,DE⊥AB,DF∥BG,由此可判断∠1=∠2,请说明理由.