题目内容
 已知:如图,AB∥CD,直线EF分别交AB、CD于点E、F,∠BEF的平分线与∠DEF的平分线相交于点P.∠P=________.
已知:如图,AB∥CD,直线EF分别交AB、CD于点E、F,∠BEF的平分线与∠DEF的平分线相交于点P.∠P=________.
90°
分析:由AB∥CD,可知∠BEF与∠DFE互补,由角平分线的性质可得∠PEF+∠PFE=90°,由三角形内角和定理可得∠P=90度.
解答:∵AB∥CD
∴∠BEF+∠DFE=180°
又∵∠BEF的平分线与∠DFE的平分线相交于点P
∴∠PEF= ∠BEF,∠PFE=
∠BEF,∠PFE= ∠DFE
∠DFE
∴∠PEF+∠PFE= (∠BEF+∠DFE)=90°
(∠BEF+∠DFE)=90°
∵∠PEF+∠PFE+∠P=180°
∴∠P=90°.
故答案为90°.
点评:本题考查综合运用平行线的性质、角平分线的定义、三角形内角和等知识解决问题的能力.
分析:由AB∥CD,可知∠BEF与∠DFE互补,由角平分线的性质可得∠PEF+∠PFE=90°,由三角形内角和定理可得∠P=90度.
解答:∵AB∥CD
∴∠BEF+∠DFE=180°
又∵∠BEF的平分线与∠DFE的平分线相交于点P
∴∠PEF=
 ∠BEF,∠PFE=
∠BEF,∠PFE= ∠DFE
∠DFE∴∠PEF+∠PFE=
 (∠BEF+∠DFE)=90°
(∠BEF+∠DFE)=90°∵∠PEF+∠PFE+∠P=180°
∴∠P=90°.
故答案为90°.
点评:本题考查综合运用平行线的性质、角平分线的定义、三角形内角和等知识解决问题的能力.

练习册系列答案
相关题目
 8、已知:如图,AB、AC分别切⊙O于B、C,D是⊙O上一点,∠D=40°,则∠A的度数等于( )
8、已知:如图,AB、AC分别切⊙O于B、C,D是⊙O上一点,∠D=40°,则∠A的度数等于( ) 已知:如图,AB,CD相交于点O,且OA•OD=OB•OC,求证:AC∥DB.
已知:如图,AB,CD相交于点O,且OA•OD=OB•OC,求证:AC∥DB.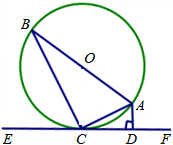 已知:如图,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.
已知:如图,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.
 29、已知,如图,AB∥CD,∠EAB+∠FDC=180°.求证:AE∥FD.
29、已知,如图,AB∥CD,∠EAB+∠FDC=180°.求证:AE∥FD. 已知:如图,AB=AC,DB=DC,求证:∠B=∠C.
已知:如图,AB=AC,DB=DC,求证:∠B=∠C.