题目内容
19.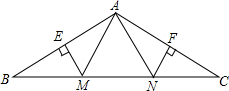 如图所示,在等腰△ABC中,∠BAC=120°,若EM和FN分别垂直平分AB和AC,垂足分别为E、F、M、N都在BC边上,且EM=FN=4,则BC的长度为( )
如图所示,在等腰△ABC中,∠BAC=120°,若EM和FN分别垂直平分AB和AC,垂足分别为E、F、M、N都在BC边上,且EM=FN=4,则BC的长度为( )| A. | 12 | B. | 16 | C. | 20 | D. | 24 |
分析 由EM和FN分别垂直平分AB和AC,可得AM=BM,AN=CN,由在等腰△ABC中,∠BAC=120°,EM=FN=4,易求得BM=CN=8,继而证得△AMN是等边三角形,则可求得MN的长,继而求得答案.
解答 解:∵在等腰△ABC中,∠BAC=120°,
∴∠B=∠C=30°,
∵EM和FN分别垂直平分AB和AC,EM=FN=4,
∴AM=BM,AN=CN,BM=2EM=8,CN=2FN=8,
∴∠BAM=∠B=30°,AM=AN=8,
∴∠AMN=∠B+∠BAM=60°,
∴△AMN是等边三角形,
∴MN=AM=AN=8,
∴BC=BM+MN+CN=24.
故选D.
点评 此题考查了线段垂直平分线的性质、等腰三角形的性质以及等边三角形的判定与性质.注意垂直平分线上任意一点,到线段两端点的距离相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.下列叙述正确的是( )
| A. | 近似数8.96×104精确到百分位 | B. | 近似数5.3万精确到千位 | ||
| C. | 近似数0.310有两个有效数字 | D. | 用科学记数法表示80500=8.05×105 |
14.下列计算错误的是( )
| A. | (-2)-(-5)=+3 | B. | (-$\frac{1}{5}$+$\frac{1}{7}$)×(-35)=(-35)×(-$\frac{1}{5}$)+(-35)×$\frac{1}{7}$ | ||
| C. | (-2)×(-3)=+6 | D. | 18÷($\frac{1}{2}$-$\frac{1}{3}$)=18÷$\frac{1}{2}$-18÷$\frac{1}{3}$ |
 如图,AF、AD分别是△ABC的高和角平分线,且∠B=32°,∠C=78°,则∠DAF=23°.
如图,AF、AD分别是△ABC的高和角平分线,且∠B=32°,∠C=78°,则∠DAF=23°.
 如图,OP平分∠MON,PE⊥OM于E,PF⊥ON于F,OA=OB,则图中全等三角形的对数为( )
如图,OP平分∠MON,PE⊥OM于E,PF⊥ON于F,OA=OB,则图中全等三角形的对数为( )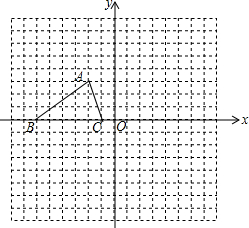 如图,已知△ABC三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
如图,已知△ABC三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).