Question

如图，在梯形ABCD中，AD∥BC，∠B=90°，AB=10cm，AD=18cm，BC=21cm，点P从点A出发，沿边AD向点D以1cm/s的速度移动，点Q从点C出发沿边CB向点B以2cm/s的速度移动，若点P与点Q同时出发，当这两点有一点运动到端点时，另一点也停止运动，没运动时间为t（秒）．
（1）求四边形APQB的面积；（用含t的代数式表示）
（2）当t为何值时，四边形PQCD为等腰梯形？
（3）连接PC，是否存在t的值，使得△PQC的面积、△PCD的面积与四边形APQB的面积同时相等？若存在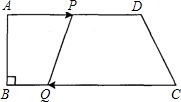，求出t的值；若不存在，说明理由．

Answer 1

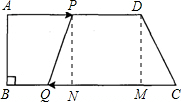解：（1）根据题意可知AP=t，BQ=21-2t，
故S_{四边形APQB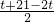}=×10=105-5t，

（2）过P作PN⊥BC于N，过D作DM⊥BC于M，
∵AD∥BC，∠B=90°，DM⊥BC，
∴四边形ABMD是矩形，AD=BM．
∴MC=BC-BM=BC-AD=3．
又∵QN=BN-BQ=AP-BQ=t-（21-2t）=3t-21．
若梯形PQCD为等腰梯形，则QN=MC．
得3t-21=3，t=8，即t=8秒时，梯形PQCD是等腰梯形．

（3）若△PQC的面积与△PCD的面积相等，则CQ×10=PD×10，
∴CQ=PD，即2t=18-t，解得t=6，此时S_△PQC=S_△PCD=×12×10=60，
∴S_APQB=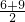×10=75，
所以不存在t的值，使得△PQC的面积、△PCD的面积与四边形APQB的面积同时相等．
分析：（1）用t表示出AP和BQ的长，然后根据梯形的面积公式进行解答，
（2）过P作PN⊥BC于N，过D作DM⊥BC于M，根据题干条件求出MC的长，用t表示出QN的长，若梯形PQCD为等腰梯形，则QN=MC，列出等式解出t的值，
（3）若△PQC的面积与△PCD的面积相等，则CQ×10=PD×10，即CQ=PD，解出t的值，然后分别求出△PQC的面积、△PCD的面积与四边形APQB的面积，验证相等是否成立．
点评：本题主要考查等腰梯形的性质，解答本题的关键是熟练掌握等腰梯形的判定定理和梯形的面积计算公式，此题难度一般．