Question

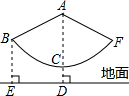
如图，秋千拉绳长3米，静止时踩板离地面0.5米，已知秋千的最大摆角∠AOB=120°，则秋千摆到最高处时踩板距离地面的高度为

2

米．

Answer 1

分析：在直角△BFO中，根据三角函数的定义就可以求出OF的长度；然后根据图中线段间的和差关系即可求得EF的长度；最后在矩形CFBD中求得BD=CF．

解答：解：根据题意知，OA=OB=3米，∠AOB=120°，AB⊥OF，则∠BOF=60°，∠OBF=30°，
在Rt△OBF△中，OF=

1

2

OB=

3

2

米；
∵OE=OA=3米，
∴EF=OE-OF=（3-

3

2

）米=

3

2

米；
∴CF=BD=EF+EC=

3

2

米+0.5米=2米，即秋千摆到最高处时踩板距离地面的高度为2米；
故答案是：2．

点评：本题考查了含30度角的直角三角形．30度角所对的直角边是斜边的一半．