题目内容
正比例函数y=k1x和反比例函数y=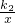 交于A(1,m),B(n,-2)两点,其中点A在第一象限,则m+n等于
交于A(1,m),B(n,-2)两点,其中点A在第一象限,则m+n等于
- A.3
- B.-1
- C.1
- D.-3
C
分析:由于正比例函数y=k1x和反比例函数y=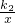 交于A(1,m),B(n,-2)两点,那么A和B在y=k1x上,也在y=
交于A(1,m),B(n,-2)两点,那么A和B在y=k1x上,也在y=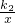 上.
上.
解答:把A(1,m),B(n,-2)两点分别代入y=k1x和y=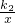 ,
,
得 ,
, ,
,
即mn=-2, .
.
于是得到 ,
,
解得 和
和 .
.
由于A在第一象限,
所以k1>0,即m>0,
所以只能取值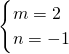 .
.
所以m+n=1.
故选C.
点评:本题综合考查反比例函数与方程组的相关知识点.先由点的坐标求函数解析式,然后解由解析式组成的方程组求出交点的坐标,体现了数形结合的思想.
分析:由于正比例函数y=k1x和反比例函数y=
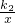 交于A(1,m),B(n,-2)两点,那么A和B在y=k1x上,也在y=
交于A(1,m),B(n,-2)两点,那么A和B在y=k1x上,也在y=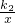 上.
上.解答:把A(1,m),B(n,-2)两点分别代入y=k1x和y=
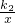 ,
,得
 ,
, ,
,即mn=-2,
 .
.于是得到
 ,
,解得
 和
和 .
.由于A在第一象限,
所以k1>0,即m>0,
所以只能取值
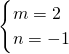 .
.所以m+n=1.
故选C.
点评:本题综合考查反比例函数与方程组的相关知识点.先由点的坐标求函数解析式,然后解由解析式组成的方程组求出交点的坐标,体现了数形结合的思想.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
 (2012•广州)如图,正比例函数y1=k1x和反比例函数y2=
(2012•广州)如图,正比例函数y1=k1x和反比例函数y2=