题目内容
已知△ABC是等腰直角三角形,∠A=90°,点D是腰AC上的一个动点,过C作CE垂直于BD的延长线,垂足为E.

(1)若BD是AC边上的中线,如图1,求 的值;
的值;
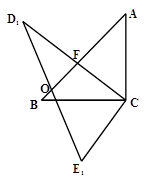
(2)若BD是∠ABC的角平分线,如图2,求 的值.
的值.

(1)若BD是AC边上的中线,如图1,求
 的值;
的值;(2)若BD是∠ABC的角平分线,如图2,求
 的值.
的值.(1) ;(2)2.
;(2)2.
 ;(2)2.
;(2)2.试题分析:设AB=AC=1,CD=x,应用勾股定理和相似三角形的判定和性质,把
 用x来表示,
用x来表示,(1)若BD是AC的中线,则CD=AD,据此求出
 的值;
的值;(2)若BD是∠ABC的角平分线,则由Rt△ABD∽Rt△EBC得
 ,据此求出
,据此求出 的值.
的值.试题解析:设AB=AC=1,CD=x,则0<x≤1,BC=
 ,AD=1-x.
,AD=1-x.在Rt△ABD中,BD2=AB2+AD2=1+(1-x)2=x2-2x+2.
由已知可得Rt△ABD∽Rt△ECD,
∴
 ,即
,即 ,∴
,∴ .
.∴
 ,0<x≤1.
,0<x≤1.(1)若BD是AC的中线,则CD=AD=x=
 ,得
,得 .
.(2)若BD是∠ABC的角平分线,则Rt△ABD∽Rt△EBC,
∴
 ,得
,得 ,即
,即 ,解得,
,解得, .
.∴
 .
.
练习册系列答案
相关题目

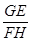 的值.
的值. 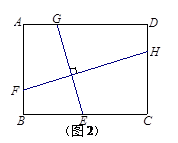
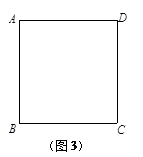
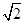 cm,CE="5cm," CD=10cm.
cm,CE="5cm," CD=10cm.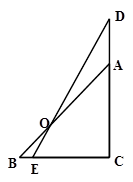
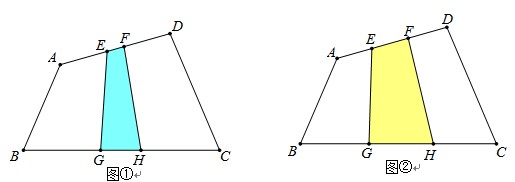
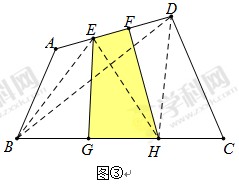
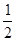 S△EBH
S△EBH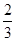 S△ABD
S△ABD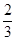 S四边形ABCD
S四边形ABCD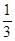 S四边形ABCD
S四边形ABCD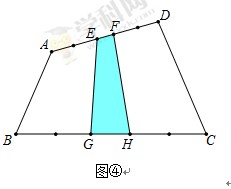
 三个顶点的坐标分别为
三个顶点的坐标分别为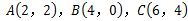 ,以原点为位似中心,将△
,以原点为位似中心,将△ 缩小,位似比为
缩小,位似比为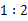 ,则线段
,则线段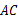 的中点
的中点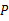 变换后对应点的坐标为_________.
变换后对应点的坐标为_________. 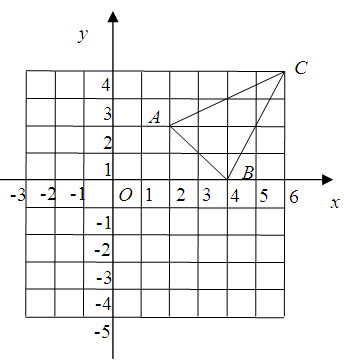
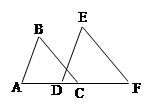





 ,那么
,那么 的值是( )
的值是( )


 的边BC上的一点,那么下列四个条件中,不能够判定△ABC与△DBA相似的是 ( )
的边BC上的一点,那么下列四个条件中,不能够判定△ABC与△DBA相似的是 ( )



