题目内容
已知:如图1,∠ACG=90°,AC=2,点B为CG边上的一个动点,连接AB,将△ACB沿AB边所在的直线翻折得到△ADB,过点D作DF⊥CG于点F.(1)当BC=
 时,判断直线FD与以AB为直径的⊙O的位置关系,并加以证明;
时,判断直线FD与以AB为直径的⊙O的位置关系,并加以证明;(2)如图2,点B在CG上向点C运动,直线FD与以AB为直径的⊙O交于D、H两点,连接AH,当∠CAB=∠BAD=∠DAH时,求BC的长.

【答案】分析:(1)根据已知及切线的判定证明得,直线FD与以AB为直径的⊙O相切;
(2)根据圆内接四边形的性质及直角三角形的性质进行分析,从而求得BC的长.
解答: 解:(1)判断:直线FD与以AB为直径的⊙O相切.
解:(1)判断:直线FD与以AB为直径的⊙O相切.
证明:如图,
作以AB为直径的⊙O;
∵△ADB是将△ACB沿AB边所在的直线翻折得到的,
∴△ADB≌△ACB,
∴∠ADB=∠ACB=90°.
∵O为AB的中点,连接DO,
∴OD=OB= AB,
AB,
∴点D在⊙O上.
在Rt△ACB中,BC= ,AC=2;
,AC=2;
∴tan∠CAB= =
= ,
,
∴∠CAB=∠BAD=30°,
∴∠ABC=∠ABD=60°,
∴△BOD是等边三角形.
∴∠BOD=60°.
∴∠ABC=∠BOD,
∴FC∥DO.
∵DF∥CG,
∴∠ODF=∠BFD=90°,
∴OD⊥FD,
∴FD为⊙O的切线.
(2)延长AD交CG于点E,
同(1)中的方法,可证点C在⊙O上;
∴四边形ADBC是圆内接四边形.
∴∠FBD=∠1+∠2.
同理∠FDB=∠2+∠3.
∵∠1=∠2=∠3,
∵∠FBD=∠FDB,
又∠DFB=90°.
∴EC=AC=2.
设BC=x,则BD=BC=x,
∵∠EDB=90°,
∴EB= x.
x.
∵EB+BC=EC,
∴ x+x=2,
x+x=2,
解得x=2 -2,
-2,
∴BC=2 -2.
-2.
点评:本题主要考查了切线的判定,圆的内接四边形等知识点,根据已知的边的长或相等角得出特殊角从而构建出特殊的直角三角形是解题的关键.
(2)根据圆内接四边形的性质及直角三角形的性质进行分析,从而求得BC的长.
解答:
 解:(1)判断:直线FD与以AB为直径的⊙O相切.
解:(1)判断:直线FD与以AB为直径的⊙O相切.证明:如图,
作以AB为直径的⊙O;
∵△ADB是将△ACB沿AB边所在的直线翻折得到的,
∴△ADB≌△ACB,
∴∠ADB=∠ACB=90°.
∵O为AB的中点,连接DO,
∴OD=OB=
 AB,
AB,∴点D在⊙O上.
在Rt△ACB中,BC=
 ,AC=2;
,AC=2;∴tan∠CAB=
 =
= ,
,∴∠CAB=∠BAD=30°,
∴∠ABC=∠ABD=60°,
∴△BOD是等边三角形.
∴∠BOD=60°.
∴∠ABC=∠BOD,
∴FC∥DO.
∵DF∥CG,
∴∠ODF=∠BFD=90°,
∴OD⊥FD,
∴FD为⊙O的切线.
(2)延长AD交CG于点E,
同(1)中的方法,可证点C在⊙O上;
∴四边形ADBC是圆内接四边形.
∴∠FBD=∠1+∠2.

同理∠FDB=∠2+∠3.
∵∠1=∠2=∠3,
∵∠FBD=∠FDB,
又∠DFB=90°.
∴EC=AC=2.
设BC=x,则BD=BC=x,
∵∠EDB=90°,
∴EB=
 x.
x.∵EB+BC=EC,
∴
 x+x=2,
x+x=2,解得x=2
 -2,
-2,∴BC=2
 -2.
-2.点评:本题主要考查了切线的判定,圆的内接四边形等知识点,根据已知的边的长或相等角得出特殊角从而构建出特殊的直角三角形是解题的关键.

练习册系列答案
相关题目
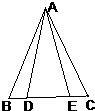 33、已知:如图,AB=AC,AD=AE,B、D、E、C在同一直线上,试判断BD与EC的大小关系,并说明理由.
33、已知:如图,AB=AC,AD=AE,B、D、E、C在同一直线上,试判断BD与EC的大小关系,并说明理由. (1997•台湾)已知:如图,AB=AC,AQ为任一弦与BC相交于P点.求证:AB为AP与AQ之比例中项.
(1997•台湾)已知:如图,AB=AC,AQ为任一弦与BC相交于P点.求证:AB为AP与AQ之比例中项. 已知:如图,DE⊥AC,BF⊥AC,且DC=AB,DC∥AB,AE=CF
已知:如图,DE⊥AC,BF⊥AC,且DC=AB,DC∥AB,AE=CF 已知:如图,DE⊥AC,BC⊥AC,AC、BC交于C,DE、AC交于E,AD、AB交于A,BC=AE.∠BAD=90°,若AB=5,则AD=
已知:如图,DE⊥AC,BC⊥AC,AC、BC交于C,DE、AC交于E,AD、AB交于A,BC=AE.∠BAD=90°,若AB=5,则AD= (1)填空:如图1,已知AB=AD,DC=BC.
(1)填空:如图1,已知AB=AD,DC=BC.