题目内容
已知△ABC中AB=AC,BC=8,其外接圆半径为5,则△ABC的周长为
- A.

- B.

- C.
 或
或
- D.以上都不对
C
分析:根据题意画出图形,由于△ABC的形状不能确定,故应分△ABC是锐角三角形和钝角三角形两种情况进行讨论.
解答: 解:当△ABC是锐角三角形时,如图1所示:
解:当△ABC是锐角三角形时,如图1所示:
过点A作AD⊥BC于点D,连接OB,
∵⊙O是△ABC的外接圆,
∴点O在直线AD上,
∵AB=AC,BC=8,
∴BD=CD= BC=
BC= ×8=4,
×8=4,
∵OB=5,
∴在Rt△OBD中,OD= =
= =3,
=3,
∴AD=OA+OD=5+3=8,
在Rt△ABD中,
AB= =
=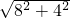 =4
=4 ,
,
∴△ABC的周长=AB+AC+BC=4 +4
+4 +8=8+8
+8=8+8 ;
;
当△ABC是锐角三角形时,如图2所示,过点A作AD⊥BC于点D,连接OB,
∵⊙O是△ABC的外接圆,
∴点O在直线AD上,
∵AB=AC,BC=8,
∴BD=CD= BC=
BC= ×8=4,
×8=4,
∵OB=5,
∴在Rt△OBD中,OD= =
= =3,
=3,
∴AD=OA-OD=5-3=2,
在Rt△ABD中,
AB= =
= =2
=2 ,
,
∴△ABC的周长=AB+AC+BC=2 +2
+2 +8=8+4
+8=8+4 .
.
∴△ABC的周长为:8+4 或8+8
或8+8 .
.
点评:本题考查的是垂径定理及勾股定理,根据题意画出图形,利用数形结合求解是解答此题的关键.
分析:根据题意画出图形,由于△ABC的形状不能确定,故应分△ABC是锐角三角形和钝角三角形两种情况进行讨论.
解答:
 解:当△ABC是锐角三角形时,如图1所示:
解:当△ABC是锐角三角形时,如图1所示:过点A作AD⊥BC于点D,连接OB,
∵⊙O是△ABC的外接圆,
∴点O在直线AD上,
∵AB=AC,BC=8,
∴BD=CD=
 BC=
BC= ×8=4,
×8=4,∵OB=5,
∴在Rt△OBD中,OD=
 =
= =3,
=3,∴AD=OA+OD=5+3=8,
在Rt△ABD中,
AB=
 =
=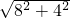 =4
=4 ,
,∴△ABC的周长=AB+AC+BC=4
 +4
+4 +8=8+8
+8=8+8 ;
;当△ABC是锐角三角形时,如图2所示,过点A作AD⊥BC于点D,连接OB,
∵⊙O是△ABC的外接圆,
∴点O在直线AD上,
∵AB=AC,BC=8,
∴BD=CD=
 BC=
BC= ×8=4,
×8=4,∵OB=5,
∴在Rt△OBD中,OD=
 =
= =3,
=3,∴AD=OA-OD=5-3=2,
在Rt△ABD中,
AB=
 =
= =2
=2 ,
,∴△ABC的周长=AB+AC+BC=2
 +2
+2 +8=8+4
+8=8+4 .
.∴△ABC的周长为:8+4
 或8+8
或8+8 .
.点评:本题考查的是垂径定理及勾股定理,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
相关题目
 19、已知△ABC中AB=AC=10,DE垂直平分AB,交AC于E.已知△BEC的周长是16,求△ABC的周长.
19、已知△ABC中AB=AC=10,DE垂直平分AB,交AC于E.已知△BEC的周长是16,求△ABC的周长.
 (2013•嘉定区一模)如图已知△ABC中AB=AC=10,BC=16,矩形DEFG的边EF在△ABC的边BC上,顶点D、G分别在AB、AC上,设DE的长为x,矩形DEFG的面积为y,求y关于x的函数关系式,并写出这个函数的定义域.
(2013•嘉定区一模)如图已知△ABC中AB=AC=10,BC=16,矩形DEFG的边EF在△ABC的边BC上,顶点D、G分别在AB、AC上,设DE的长为x,矩形DEFG的面积为y,求y关于x的函数关系式,并写出这个函数的定义域.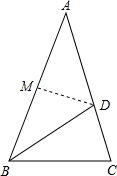 如图,已知△ABC中 AB=AC,∠A=36°,使点A、B重合对折,折痕为MD,连接BD.若△BCD的周长为5,BC=2.
如图,已知△ABC中 AB=AC,∠A=36°,使点A、B重合对折,折痕为MD,连接BD.若△BCD的周长为5,BC=2.