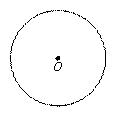
题目内容
已知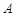 、
、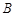 、
、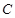 三点均在
三点均在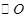 上,且
上,且 是等边三角形.
是等边三角形.
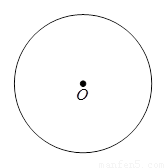
(1)如图,用直尺和圆规作出 ;(不写作法,保留作图痕迹)
;(不写作法,保留作图痕迹)
(2)若点 是
是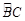 上一点,连接
上一点,连接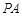 、
、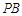 、
、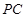 .探究
.探究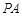 、
、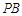 、
、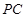 之间的等量关系并说明理由.
之间的等量关系并说明理由.
【答案】
PA=PD+AD=PB+PC.
【解析】
试题分析:(1)如图; 2分

(2)PA=PB+PC.理由如下: 3分
如图,在PA上取点D,使得PD=PC,连接CD.
∵ △ACB是等边三角形,
∴ AB=BC=CA,∠APC=∠ABC=60°.
∴ △PCD是等边三角形. 5分
∴ CD=CP.
∵ ∠ACD+∠DCB=60°,
∠BCP+∠DCB=60°,
∴∠ACD=∠BCP
∴ △CAD≌△CBP. 7分
∴ AD=BP.
∴ PA=PD+AD=PB+PC.
考点:全等三角形的性质和判定
点评:解答本题的关键是熟练掌握判定两个三角形全等的一般方法:SSS、SAS、ASA、AAS、HL,注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
 (2013•鼓楼区一模)已知A、B、C三点均在⊙O上,且△ABC是等边三角形.
(2013•鼓楼区一模)已知A、B、C三点均在⊙O上,且△ABC是等边三角形.
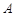 、
、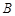 、
、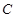 三点均在
三点均在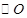 上,且
上,且 是等边三角形.
是等边三角形.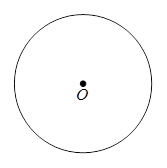
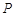 是
是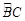 上一点,连接
上一点,连接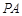 、
、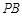 、
、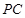 .探究
.探究 已知A、B、C三点均在⊙O上,且△ABC是等边三角形.
已知A、B、C三点均在⊙O上,且△ABC是等边三角形. 上一点,连接PA、PB、PC.探究PA、PB、PC之间的等量关系并说明理由.
上一点,连接PA、PB、PC.探究PA、PB、PC之间的等量关系并说明理由.