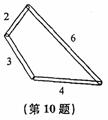
题目内容
在平面直角坐标系中,O为原点,点A(﹣2,0),点B(0,2),点E,点F分别为OA,OB的中点.若正方形OEDF绕点O顺时针旋转,得正方形OE′D′F′,记旋转角为α.
(1)如图①,当α=90°时,求AE′,BF′的长;
(2)如图②,当α=135°时,求证AE′=BF′,且AE′⊥BF′;21世纪教育网
(3)直线AE′与直线BF′相交于点P,当点P在坐标轴上时,分别表示出此时点E′、D′、F′的坐标(直接写出结果即可).www-2-1-cnjy-com
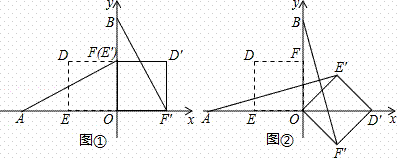
解:(1)当α=90°时,点E′与点F重合,如图①.
∵点A(﹣2,0)点B(0,2),
∴OA=OB=2.
∵点E,点F分别为OA,OB的中点,
∴OE=OF=1
∵正方形OE′D′F′是正方形OEDF绕点O顺时针旋转90°得到的,
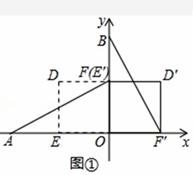 ∴OE′=OE=1,OF′=OF=1.
∴OE′=OE=1,OF′=OF=1.
在Rt△AE′O中,
AE′=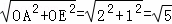 .
.
在Rt△BOF′中,
BF′=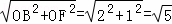 .
.
∴AE′,BF′的长都等于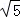 . ———————————————4分
. ———————————————4分
(2)当α=135°时,如图②.
∵正方形OE′D′F′是由正方形OEDF绕点O顺时针旋转135°所得,
∴∠AOE′=∠BOF′=135°.
在△AOE′和△BOF′中,
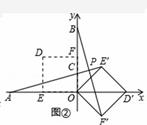
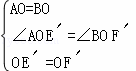 ,
,
∴△AOE′≌△BOF′(SAS).
∴AE′=BF′,且∠OAE′=∠OBF′.
∵∠ACB=∠CAO+∠AOC=∠CBP+∠CPB,∠CAO=∠CBP,
∴∠CPB=∠AOC=90°
∴AE′⊥BF′.——————————————————————9分
(3)点E′(2,0)、D′(2,-2)、F′(0,-2)……12分

练习册系列答案
相关题目
 ,则
,则 的值为…………………………………………………【 】
的值为…………………………………………………【 】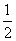 B.﹣
B.﹣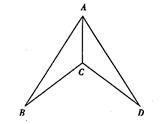
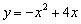 上的概率为( )
上的概率为( )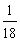 B.
B.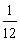 C.
C. D.
D.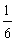
 与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转90°后得
与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转90°后得 ,则点
,则点 的坐标是
的坐标是