题目内容
18.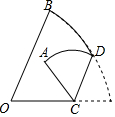 如图,在扇形AOB中,∠AOB=60°,AO=6,点D为$\widehat{AB}$的中点,C为半径OA上一动点(点A除外),沿CD对折后点A恰好落在扇形AOB的边线OB或OA上,AC的长可以是6-3$\sqrt{3}$或6或9-3$\sqrt{3}$.
如图,在扇形AOB中,∠AOB=60°,AO=6,点D为$\widehat{AB}$的中点,C为半径OA上一动点(点A除外),沿CD对折后点A恰好落在扇形AOB的边线OB或OA上,AC的长可以是6-3$\sqrt{3}$或6或9-3$\sqrt{3}$.
分析 根据点A′落在半径OA上.可以画出相应的图形,可知点A与点A′关于点CD对称,从而可以得到DA′=DA,由点C为弧AB的中点,∠AOB=60°,OD=OA=6,可以求得OC的长,从而可以求得AC的长;
根据点A′落在半径OB上,画出相应的图形,由C为半径OB上一动点(点A除外),设点A关于直线CD的对称点为A′,可知DB=DA′=DA,由点D为弧AB的中点,∠AOB=60°,OD=OA=6,可以求得DF和AF的长,从而可以求得BA′的长,进而得到A′C的长;根据题意A′C的长与AC的长相等,可以求得AC的长.
解答  解:①当点E落在半径OA上时,连接OD,如图1所示,
解:①当点E落在半径OA上时,连接OD,如图1所示,
∵∠ACD=90°,∠AOB=60°,点D为弧AB的中点,点A(2,0),
∴∠COD=30°,OA=OD=6,
∴OC=OD•cos30°=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,
∴AC=OA-OC=6-3$\sqrt{3}$;
②如图2,沿CD对折后点A恰好落在边线OB上,且A′和B重合时,
则C和O重合,此时,AC=OA=6;
③沿CD对折后点A恰好落在边线OB上,且A′和B不重合时,如图3;
连接OD、BD、AD,作DF⊥OA于F, ∵∠AFD=90°,∠AOB=60°,点D为弧AB的中点,
∵∠AFD=90°,∠AOB=60°,点D为弧AB的中点,
∴∠AOD=∠BOD=30°,∠OAD=∠OBD,
∵OA=OD=6,
∴DF=OD•sin30°=6×$\frac{1}{2}$=3,∠OAD=75°,
∴OF=OD•cos30°=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,
∴AF=OA-OD=6-3$\sqrt{3}$,
∵DA′=DA=DB,∠OAD=∠OBD=75°,
∴BA′=2AF=12-6$\sqrt{3}$,∠DA′B=∠OBD=75°,
∴OA′=OB-BA′=6-(12-6$\sqrt{3}$)=6$\sqrt{3}$-6,
∵∠CA′D=∠CAD=75°, ∴∠BA′C=150°,
∴∠BA′C=150°,
∴∠OA′C=30°,
∴∠A′CO=90°,
∴CA′=OA′•sin60°=(6$\sqrt{3}$-6)×$\frac{\sqrt{3}}{2}$=9-3$\sqrt{3}$,
∴AC=CA′=9-3$\sqrt{3}$.
故答案为:6-3$\sqrt{3}$或6或9-3$\sqrt{3}$.
点评 本题考查圆的综合题、特殊角的三角函数值,解题的关键是明确题意,画出相应的图形,找出所求问题需要的条件,利用数形结合的思想解答问题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 2017 | B. | -2017 | C. | $\frac{1}{2017}$ | D. | -$\frac{1}{2017}$ |
| A. |  | B. |  | C. |  | D. |  |
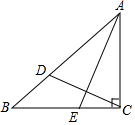 如图,Rt△ACB中,∠ACB=90°,AC=BC,E是BC边上的一点,连接AE,将△ACE沿AE折叠,使C点落在AB边上的D处,连接CD,若S△BCD=4,则AE的长为( )
如图,Rt△ACB中,∠ACB=90°,AC=BC,E是BC边上的一点,连接AE,将△ACE沿AE折叠,使C点落在AB边上的D处,连接CD,若S△BCD=4,则AE的长为( )| A. | 2 | B. | 4 | C. | 4$\sqrt{2}$ | D. | 8$\sqrt{2}$ |
| A. | 30 cm2 | B. | 15 cm2 | C. | 30π cm2 | D. | 15π cm2 |
| A. | 有两个相等的实数根 | B. | 只有一个实数根 | ||
| C. | 没有实数根 | D. | 有两个不相等的实数根 |
| A. |  | B. |  | C. |  | D. |  |
| A. |  | B. |  | C. |  | D. |  |