题目内容
初三数学课本上，用“描点法”画二次函数y=ax2+bx+c的图象时，列了如下表格：
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … |  | -4 | 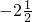 | -2 | | … |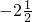
-4
分析：由表格可知，（0，-2
），（2，-2）是抛物线上两对称点，可求对称轴x=1，再利用对称性求出横坐标为3的对称点（-1，-4）即可．
解答：观察表格可知，当x=0或2时，y=-2，
根据二次函数图象的对称性，
（0，-2），（2，-2）是抛物线上两对称点，
对称轴为x=
=1，顶点（1，-2），
根据对称性，x=3与x=-1时，函数值相等，都是-4．
点评：观察二次函数的对应值的表格，关键是寻找对称点，对称轴，利用二次函数的对称性解答．
分析：由表格可知，（0，-2
），（2，-2）是抛物线上两对称点，可求对称轴x=1，再利用对称性求出横坐标为3的对称点（-1，-4）即可．解答：观察表格可知，当x=0或2时，y=-2
，根据二次函数图象的对称性，
（0，-2
），（2，-2）是抛物线上两对称点，对称轴为x=
=1，顶点（1，-2），根据对称性，x=3与x=-1时，函数值相等，都是-4．
点评：观察二次函数的对应值的表格，关键是寻找对称点，对称轴，利用二次函数的对称性解答．
练习册系列答案
备战中考寒假系列答案
相关题目
初三数学课本上，用“描点法”画二次函数y=ax2+bx+c的图象时，列了如下表格：
根据表格上的信息回答问题：该二次函数y=ax2+bx+c在x=3时，y= ．
| x | … | -2 | -1 | 0 | 1 | 2 | … | ||||||
| y | … | -6
|
-4 | -2
|
-2 | -2
|
… |
初三数学课本上，用“描点法”画二次函数y=ax2+bx+c的图象时，列了如下表格：
根据表格中的信息回答：关于x的一元二次方程ax2+bx+c=-4的解为 ．
| x | … | -2 | -1 | 0 | 1 | 2 | … | ||||||
| y | … | -6
|
-4 | -2
|
-2 | -2
|
… |
初三数学课本上，用“描点法”画二次函数y=ax2+bx+c的图象时，列了如下表格：
根据表格上的信息回答：该二次函数y=ax2+bx+c在y=-4时，x= ．
| x | … | -2 | -1 | 0 | 1 | 2 | … | ||||||
| y | … | -6
|
-4 | -2
|
-2 | -2
|
… |
的图象时，列了如下表格：
时，