题目内容
若α为锐角，tanα=4，求
的值．
解：由tanα=4知，如果设a=4x，则b=x，结合a2+b2=c2得c=
x；
∴sinα=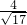
，cosα=
，
∴=
=-
．
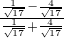分析：首先根据已知条件设出直角三角形的两条直角边的长，再根据勾股定理求出斜边的长，由三角函数的定义求出cosαsinα的值，最后代入即可．
点评：利用锐角三角函数的定义，通过设参数的方法求三角函数值．
x；∴sinα=
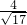，cosα=，∴
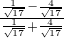==-．分析：首先根据已知条件设出直角三角形的两条直角边的长，再根据勾股定理求出斜边的长，由三角函数的定义求出cosαsinα的值，最后代入即可．
点评：利用锐角三角函数的定义，通过设参数的方法求三角函数值．
练习册系列答案
相关题目
下列说法中，正确的是（ ）
| A、在Rt△ABC中，锐角A的两边都扩大5倍，则cosA也扩大5倍 | ||||
| B、若45°＜α＜90°，则sinα＞1 | ||||
| C、cos30°+cos45°=cos（30°+45°） | ||||
D、若α为锐角，tanα=
|
（2012•思明区质检）如图，平行四边形ABCD中，AB=8，BC=10，∠B为锐角，tan∠B=