题目内容
22、已知在矩形ABCD中，对角线AC，BD相交于点O，△AOD与△COD的周长的和是116，差是4，两条对角线长的和是80，求矩形的各边长和面积．
分析：根据矩形的对角线相等且互相平分，可求得OA=OD=OC=20，进而根据△AOD与△COD的周长的关系求出矩形的长和宽，进而求得矩形的面积．
解答：
解：如图；
由于矩形的对角线相等且互相平分，得OA=OD=OC=20；
设AD=x，CD=y，依题意有：
x+20+20+20+20+y=116，且y-x=4；
解得x=16，y=20；
S矩形=20×16=320；
故：矩形各边长分别为20、16、20、16；矩形面积为320．
解：如图；由于矩形的对角线相等且互相平分，得OA=OD=OC=20；
设AD=x，CD=y，依题意有：
x+20+20+20+20+y=116，且y-x=4；
解得x=16，y=20；
S矩形=20×16=320；
故：矩形各边长分别为20、16、20、16；矩形面积为320．
点评：此题主要考查了矩形的性质：矩形的对角线相等且互相平分．
练习册系列答案
新编小学单元自测题系列答案
字词句段篇系列答案
相关题目
，E，F三点共线时，两点同时停止运动．设点E移动的时间为t（秒）．
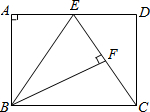（2012•德庆县一模）如图，已知在矩形ABCD中，E是AD上的一点，连接EC，BC=CE，BF⊥EC于点F．