题目内容
 如图.⊙0的半径为2,点A的坐标为(2.2
如图.⊙0的半径为2,点A的坐标为(2.2 ).直线AB为⊙O的切线,B为切点,则点B的坐标为
).直线AB为⊙O的切线,B为切点,则点B的坐标为
- A.(-
 ,
, )
) - B.(-l,
 )
) - C.(-
 ,
, )
) - D.(-
 、1)
、1)
B
分析:过B作BE⊥x轴于E,过A作AD⊥x轴于D,求出∠AOD=60°,根据HL证Rt△ABO≌Rt△ADO,求出∠AOB=60°,求出∠BOE=60°,求出∠EBO=30°,根据OB=2,求出OE、BE即可.
解答:过B作BE⊥x轴于E,过A作AD⊥x轴于D,
∵A(2,2 ),
),
∴OD=2=OB,AD=2 ,
,
在Rt△AOD中,tan∠AOD=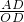 =
=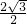 =
= ,
,
∴∠AOD=60°,
∵AD⊥x轴,AB切⊙O于B,
∴∠ADO=∠ABO=90°,
在Rt△ABO和Rt△ADO中
 ,
,
∴Rt△ABO≌Rt△ADO,
∴∠AOD=∠AOB=60°,
∴∠BOE=60°,
∴∠EBO=30°,
∴OE=1,
由勾股定理得:BE= ,
,
∴B(-1, ),
),
故选B.
点评:本题考查了全等三角形的性质和判定,勾股定理,切线的性质,锐角三角函数值等知识点的运用,关键是求出OE和BE的长,主要考查学生运用定理进行推理和计算的能力.
分析:过B作BE⊥x轴于E,过A作AD⊥x轴于D,求出∠AOD=60°,根据HL证Rt△ABO≌Rt△ADO,求出∠AOB=60°,求出∠BOE=60°,求出∠EBO=30°,根据OB=2,求出OE、BE即可.
解答:过B作BE⊥x轴于E,过A作AD⊥x轴于D,

∵A(2,2
 ),
),∴OD=2=OB,AD=2
 ,
,在Rt△AOD中,tan∠AOD=
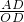 =
=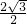 =
= ,
,∴∠AOD=60°,
∵AD⊥x轴,AB切⊙O于B,
∴∠ADO=∠ABO=90°,
在Rt△ABO和Rt△ADO中
 ,
,∴Rt△ABO≌Rt△ADO,
∴∠AOD=∠AOB=60°,
∴∠BOE=60°,
∴∠EBO=30°,
∴OE=1,
由勾股定理得:BE=
 ,
,∴B(-1,
 ),
),故选B.
点评:本题考查了全等三角形的性质和判定,勾股定理,切线的性质,锐角三角函数值等知识点的运用,关键是求出OE和BE的长,主要考查学生运用定理进行推理和计算的能力.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 如图,⊙O的半径为5,AB=5
如图,⊙O的半径为5,AB=5 如图,⊙O的半径为3,直径AB⊥弦CD,垂足为E,点F是BC的中点,那么EF2+OF2=
如图,⊙O的半径为3,直径AB⊥弦CD,垂足为E,点F是BC的中点,那么EF2+OF2= 如图,⊙O的半径为
如图,⊙O的半径为 如图,⊙O的半径为13cm,弦AB∥CD,两弦位于圆心O的两侧,AB=24cm,CD=10cm,求AB和CD的距离.
如图,⊙O的半径为13cm,弦AB∥CD,两弦位于圆心O的两侧,AB=24cm,CD=10cm,求AB和CD的距离. 如图,⊙O的半径为5,P是弦MN上的一点,且MP:PN=1:2.若PA=2,则MN的长为
如图,⊙O的半径为5,P是弦MN上的一点,且MP:PN=1:2.若PA=2,则MN的长为