��Ŀ����
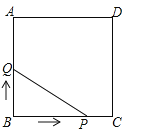
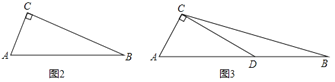
����Ŀ����ͼ1��![]() ��
��![]() �ǵ���ֱ�������Σ���
�ǵ���ֱ�������Σ���![]() ��
��![]() ����
����![]() �ϣ�����
�ϣ�����![]() ��
��![]() ���ӳ��߽��ڵ�
���ӳ��߽��ڵ�![]() .
.
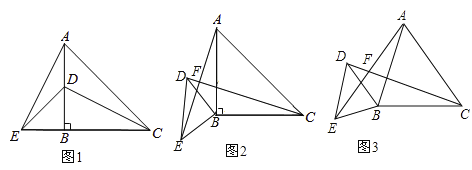
��1��д���߶�![]() ��
��![]() ��������ϵ����˵������.
��������ϵ����˵������.
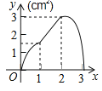
��2������ͼ1�е�![]() �Ƶ�
�Ƶ�![]() ��ʱ����תһ����ǣ���ͼ2��ʾ����ͼ2�е��߶�
��ʱ����תһ����ǣ���ͼ2��ʾ����ͼ2�е��߶�![]() ��
��![]() ֮����������������λ�ù�ϵ����˵������.
֮����������������λ�ù�ϵ����˵������.
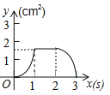
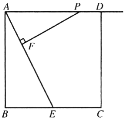
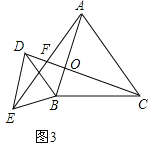
��3����չ������ͼ1�е�![]() �Ƶ�
�Ƶ�![]() ��ʱ����תһ����ǣ�����
��ʱ����תһ����ǣ�����![]() ����Ϊ��
������![]() ��
��![]() Ϊ��ǣ������������������䣬��ͼ3��ʾ���ʣ��߶�
Ϊ��ǣ������������������䣬��ͼ3��ʾ���ʣ��߶�![]() ��
��![]() ����ֱ�ߵļнǴ�С�Ƿ�����ͼ�ε���ת�������仯�������䣬��ֵ���٣�
����ֱ�ߵļнǴ�С�Ƿ�����ͼ�ε���ת�������仯�������䣬��ֵ���٣�
���𰸡���1��![]() . ���ɼ���������2��
. ���ɼ���������2��![]() �����ɼ���������3���߶�
�����ɼ���������3���߶�![]() ��
��![]() ����ֱ�ߵļнǴ�С���䣬
����ֱ�ߵļнǴ�С���䣬![]() . ���ɼ�����
. ���ɼ�����
��������
(1)����ȫ�������ε��ж�(SAS)֤��![]() ���Ӷ���֪
���Ӷ���֪![]() ��
��
(2)����ȫ�������ε��ж�(SAS)ͬ����֤��![]() ,��
,��![]() ��
��![]() �п�֤��
�п�֤��![]() ��
��
(3)����ȫ�������ε��ж�(SAS)ͬ����֤��![]() ����
����![]() ��
��![]() �п�֤��
�п�֤��![]() ��
��
��1�����ۣ�![]() .
.
���ɣ���ͼ1�У�
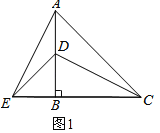
��![]() ��
��![]() ��
�У�
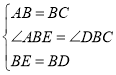 ��
��
��![]()
��![]() .
.
��2�����ۣ�![]() ��
��
���ɣ���ͼ2�У���![]() ��
��![]() ��
��![]() .
.
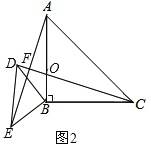
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
�У�
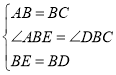 ��
��
��![]()
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() .
.
��3���߶�![]() ��
��![]() ����ֱ�ߵļнǴ�С���䣬
����ֱ�ߵļнǴ�С���䣬![]() .
.
���ɣ���ͼ3�У���![]() ��
��![]() ��
��![]() .
.
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
�У�
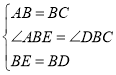 ��
��
��![]() ��
��
��img src="https://thumb.zyjl.cn/questionBank/Upload/2020/11/27/10/9ad08ab3/SYS202011271008462374325884_DA/SYS202011271008462374325884_DA.027.png" width="108" height="20" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />��
��![]() ��
��
��![]() .
.