Question

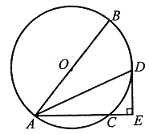
【题目】如图1，在△OMN中，∠MON=90°，OM=6cm，∠OMN=30°.等边△ABC的顶点B与点O重合，BC在OM上，点A恰好在MN上.

（1）求等边△ABC的边长；

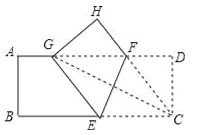
（2）如图2,将等边△ABC沿OM方向以1cm/s的速度平移,边AB、AC分别与MN交于点E、F,在△ABC平移的同时,点P从△ABC的顶点B出发,以2cm/s的速度沿折线B→A→C运动,当点P达到点C时,点P停止运动,△ABC也随之停止平移．设△ABC平移时间为t（s）

①用含t的代数式表示AE的长,并写出t的取值范围；

②在点P沿折线B→A→C运动的过程中,是否在某一时刻,点P、E、F组成的三角形为等腰三角形?若存在,求出此时t值；若不存在,请说明理由．

Answer 1

【答案】（1）3cm;(2)①（）②t值为或2或

【解析】试题分析：（1）根据，∠OMN=30°和△ABC为等边三角形，求证△OAM为直角三角形，然后即可得出答案．

（2）①由直角三角形的性质得出ON=2，MN=4．证明△OMN∽△BEM，得出对应边成比例，得出BE，即可得出AE的长，容易得出t的取值范围；

②△PEF为等腰三角形，分情况讨论，求出t的值，如果在0＜t＜3这个范围内就存在，否则就不存在．

试题解析：（1）∵△ABC为等边三角形，

∴∠AOC=60°，

又∵∠OMN=30°

∴∠OAM=90°，OA⊥MN，

即△OAM为直角三角形，

∴OA=OM=3cm，

即等边△ABC的边长为3cm．

（2）①∵BM=6-t，OM=6cm，∠OMN=30°，

∴ON=2，MN=4．

∵∠M=∠M，∠N=∠MBE=60°，

∴△OMN∽△BEM，

∴，即，

∴BE=，

∴AE=AB-BE=（0≤t≤3）；

②存在；理由如下：

分4种情况：

（a）当点P在线段AB上时，点P在AB上运动的时间0≤t≤，

∵△PEF为等腰三角形，∠PEF=90°

∴PE=EF，

∵∠A=60°，∠AFE=30°，

∴EF=AE=（3-BE）=（3-）=t，

∴=t或=t，

解得t=或＞（故舍去），

（b）当点P在AF上时，

若PE=PF时，点P为EF的垂直平分线与AC的交点，

此时P为直角三角形PEF斜边AF的中点，

∴PF=AP=2t-3，

∵点P从△ABC的顶点B出发，以2cm/s的速度沿折线B→A→C运动，

∴0＜t＜3，在直角三角形中，cos30°=，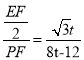

解得：t=2，

若FE=FP，

AF= ，

则t-（2t-3）=t，

解得：t=12-6；

（c）当PE=EF，P在AE上时无解，

（d）当P点在CF上时，AP=2t-3，AF=t，则PF=AP-AF=t-3=EF，所以t-3=t，

解得 t=12+6＞3，不合题意，舍去．

综上，存在t值为或12-6或2时，△PEF为等腰三角形．