��Ŀ����
����Ŀ�����ǽ�ʹ�ú���ֵΪ����Ա�����ֵ��Ϊ���������ֵ����ʱ�ĵ��Ϊ��������㣮���磬���ں���![]() ����
����![]() ���ɵ�
���ɵ�![]() �����Ǿ�˵1�Ǻ���
�����Ǿ�˵1�Ǻ���![]() �����ֵ����
�����ֵ����![]() �Ǻ���
�Ǻ���![]() ����㣮
����㣮
��֪���κ���![]() ��
��
��1�����������������غϵ����ʱ����k��ȡֵ��Χ��
��2����������������㶼�������㣬������k��ֵ��
��3����k<0ʱ���ڣ�2���������£��������������ֱ��ǵ�A��B����A�ڵ�B����ࣩ�������κ�����ͼ���ڵ�A��B��IJ��֣�����A�͵�B������ƽ��![]() ����λ��õ���ͼ���Ϊ
����λ��õ���ͼ���Ϊ![]() ��ͬʱ��ֱ��
��ͬʱ��ֱ��![]() ����ƽ��
����ƽ��![]() ����λ������ͼ��ش𣺵�ƽ�ƺ��ֱ����ͼ��
����λ������ͼ��ش𣺵�ƽ�ƺ��ֱ����ͼ��![]() �й�����ʱ����
�й�����ʱ����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
���𰸡���1����![]() ��
��![]() ʱ�����κ������������غϵ���㣮
ʱ�����κ������������غϵ���㣮
��2��![]() ��
��
��3��![]() ��
��
��������
��1�����������֪����0��![]() ����ü��ɣ���2����y=0���ⷽ�̵�
����ü��ɣ���2����y=0���ⷽ�̵�![]() ��
��![]()
�����������֪![]() �����������ɵó�kֵ����3����k<0���ɵ�
�����������ɵó�kֵ����3����k<0���ɵ�![]() �����ɵó�����������ʽ���ó�A��B�������꣬��ʾ��ƽ�ƺ�ĵ�Ϊ
�����ɵó�����������ʽ���ó�A��B�������꣬��ʾ��ƽ�ƺ�ĵ�Ϊ![]() ��
��![]() ��ƽ�ƺ�Ľ���ʽ
��ƽ�ƺ�Ľ���ʽ![]() ����ʽ�����nֵ�����ɵó���Χ.
����ʽ�����nֵ�����ɵó���Χ.
��:��1��![]()
![]()
�����κ������������غϵ����
��![]()
��![]()
����![]() ��
��![]() ʱ�����κ������������غϵ���㣮
ʱ�����κ������������غϵ���㣮
��2���ⷽ�̵ã� ,
,
��![]() ��
��![]() ��
��
��������������㶼��������![]() ��������
��������
��![]() ��������
��������
��![]() ��
��
��3����k<0��
��![]() ��
��
��![]() ��
��![]() ��
��
���������������ֱ���A�� B����A�ڵ�B����ࣩ��
��![]() ��
��![]() ��
��
��ƽ�ƺ�ĵ�Ϊ![]() ��
��![]() ��
��
ƽ�ƺ�Ľ���ʽΪ![]() ��
��
��![]() ���
���![]() ��
��
![]() ���
���![]() ��
��
��![]() ��
��

����Ŀ��ij����ѧ��ȤС��Ժ���y��|x2��2x|��ͼ������ʽ�����̽����̽���������£��벹��������
��1���Ա���x��ȡֵ��Χȡ��ȫ��ʵ����x��y�ļ����Ӧֵ�б����£�����m���� ����
x | ���� | ��1 | ��0.5 | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | ���� |
y | ���� | 3 | m | 0 | 0.75 | 1 | 0.75 | 0 | 1.25 | 3 | ���� |
��2�������ϱ����ݣ�����ͼ��ʾ��ƽ��ֱ������ϵ����㣬���ڻ����˺���ͼ���һ���֣��뻭���ú���ͼ�����һ���֣�
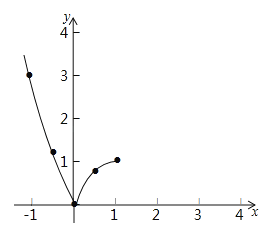
��3���۲캯��ͼ��д��������һ�������� ����
��4����һ��̽������ͼ�������⣺
�ٷ���|x2��2x|��![]() ���� ����ʵ������
���� ����ʵ������
���ڣ�2���ʵ�ƽ��ֱ������ϵ�л���ֱ��y����x+1������ͼ��д������|x2��2x|����x+1��һ��������ԼΪ�� ��������ȷ��0.1��