题目内容
如图，在梯形PMNQ中，PQ∥MN，对角线PN和MQ相交于点O，并把梯形分成四部分，记这四部分的面积分别为S1、S2、S3、S4．试判断S1+S2和S3+S4的大小关系，并证明你的结论．
解：S1+S2＞S3+S4．
证明：设PQ=m，MN=n，∵△PMN和△QMN同底等高，
∴S△PMN=S△QMN，
∴S3+S2=S4+S2，即：S3=S4．
∵△POQ∽△NOM，
∴S1：S2=（OQ：OM）2=m2：n2，∴
．
∵S1：S3=OQ：OM=m：n，∴
．
∴
=
．
∵
，∴S1+S2＞S3+S4．
分析：设PQ=m，MN=n，根据同底等高判断△PMN和△QMN的面积相等，然后根据三角形的相似比，把s2，s3，s4都用s1以及m，n表示出来，然后用（S1+s2）-（S3+s4）化简结果后看谁大谁小．
点评：本题考查相似三角形的判定和性质以及三角形面积的等底等高或者等高等情况的特性，本题最后做一个差的运算来判断大小．
证明：设PQ=m，MN=n，∵△PMN和△QMN同底等高，
∴S△PMN=S△QMN，
∴S3+S2=S4+S2，即：S3=S4．
∵△POQ∽△NOM，
∴S1：S2=（OQ：OM）2=m2：n2，∴
．∵S1：S3=OQ：OM=m：n，∴
．∴
=．∵
，∴S1+S2＞S3+S4．分析：设PQ=m，MN=n，根据同底等高判断△PMN和△QMN的面积相等，然后根据三角形的相似比，把s2，s3，s4都用s1以及m，n表示出来，然后用（S1+s2）-（S3+s4）化简结果后看谁大谁小．
点评：本题考查相似三角形的判定和性质以及三角形面积的等底等高或者等高等情况的特性，本题最后做一个差的运算来判断大小．
练习册系列答案
相关题目
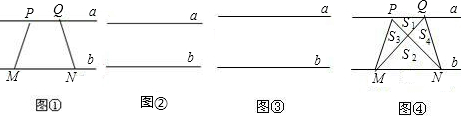
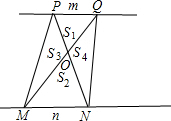如图，若梯形PMNQ是一块绿化地，梯形上底PQ=m，下底MN=n，现在计划把价格不同的两种花草种植在S1、S2、S3、S4四块地里，使得价格相同的花草不相邻，为了节省费用，园艺师应该把哪两块地种植较便宜的花草？通过计算说明你的理由．
如图，在梯形PMNQ中，PQ∥MN，对角线PN和MQ相交于点O，并把梯形分成四部分，记这四部分的面积分别为S1、S2、S3、S4．试判断S1+S2和S3+S4的大小关系，并证明你的结论．